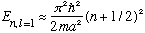1) Remember, to find the commutator of two operators, you let the commutator operate on some arbitrary f (and then pull out the f at the end, to leave a pure operator eq'n). You'll need to remember the "chain rule" involving the gradient acting on a product of scalar functions...

2a) When in doubt, you can always write out L_z explicitly in terms of x's, y's, d/dx's, and d/dys, and then, like in #1, let the commutators operate on some arbitrary function...

2b) This is a simple exercise in expanding sin's and cos's. The only trick is deciding how many terms you need in your starting expansions to get two (nonzero ones) left over at the end...

2c) Write (simple) formulas giving x, y, and z in terms of r, theta, phi. This should help.

3b) Gas. p.180 (and 179!) should help. I get 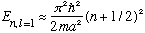if n is large. (Are the correct energies slightly less than this, or slightly larger? There's a definite, simple answer!)

4) Since l=0, the radial equation (for u, not R) should be familiar (and easy! )What must u(r) be inside r<a, by inspection? What's the GENERAL solution outside r>a? There are many different ways to write this function, the generic form used by Gas in e.g. Eq. 10-89 should allow you to "read off" the phase shift without any real effort at all.