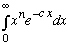
It will be worth your while to figure out how to evaluate

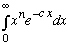
(with n an integer) before starting this homework set, you'll use it a couple of times, this week (Just do it by parts, repeatedly, there's a very simple answer)

1) Remember way back to Gas. problem 4-5. This is a 3-D version of exactly the same thing! Almost no work is required - you can use Gas. Eq 12-30 to simply write down any radial wavefunctions you need. (You have one integral to do, which is not hard given the formula at the top...)

I get an answer between 60 and 85%

2) No calculations required beyond squaring and adding numbers for this one!

3) This problem is fundamentally the same idea as number 1.

(You may look at the radial integral and think you could do it analytically by completion of squares, but that won't work. Do you see why not?)

4) Again, the integral at the top of the page will come in repeatedly.

(You can, of course, check your answers with Gas. 12-36 if you want, just don't use those formulas to find the answers.)

Extra Credit:

To work this one through all the way is quite a bit of work, but it will certainly teach you a lot about solving for real potentials in 3-D, and solidify the ideas and techniques introduced to solve the hydrogen problem! The order of procedure would be something like this:

Set up the radial equation.

Convert to unitless variables.

Find.the "asymptotic" behaviour at small and large r.

Pull out the asymptotic form, to leave behind a 2nd order ODE for what's left over.

To see the equation for Laguerre Polynomials appear, you may need at this point to switch variables (the trick is to define a new variable z=r^2).

In the end, you can find the energies (easy), and degeneracies (more tricky)

Back to this week's homework.