1) This is a true 2-particle problem, you can't reduce it to a 1 particle problem (because there's an external potential for both of them.)

You can just write down the answers in terms of the square well wave functions, no real calculations are required anywhere in this problem! You do have to think about what the symmetry does to restrict your allowed states.

I get a different ground state energy for parts i and ii, but I get the same ground state energies (and wave functions!) for ii and iii. (The answer for the wave function in part iii-c is ambiguous, though the energy is not.)

2) This is effectively a one particle problem, if you move to relative coordinates, because the potential depends only on the distance between the particles, x. Think about what V(x) looks like. It's a very familiar potential! (Perhaps one small tricky feature is that x can be negative.)

Once again, this problem is just a thinker - no real calculations are required. I get for parts a and c, but not for part b.

3) This is a slightly more challenging problem. (Not conceptually, but it may exercise your ability to do a bit of involved algebra) Don't try to do it "quickly" on scratch paper - be careful and neat, go slow, give yourself plenty of space, get the algebra right the first time! It helps if you set the problem up with bras and kets and simplify as much as possible before trying to evaluate any integrals.

Also, you DID all the relevant integrals in the Ch. 7 homework where you found <n|x^2|n> for a harmonic oscillator (I hope you got ),

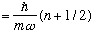and you also (hopefully) found .

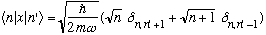If you're stumped, Griffith's Ch. 5 covers this pretty nicely. (He doesn't specialize to a harmonic oscillator, but simplifies the result formally to single particle integrals that you can easily do)

Back to this week's homework.