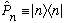Issued Wed, Oct 22 Due Wed, Oct 29

(Required reading for this week: Finish Gas. Ch. 6 , start Ch. 7

There are HINTS for this homework.

1) Gas. 6-2 and Gas 6-6

2) Gas 6-8 and Gas 6-10

3) Gas 6-3 and Gas 6-9

4) In class, we defined a projection operator into the "n" direction by 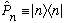, where "n" is the n'th normalized basis function

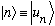
a) Show that .

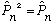b) Find the eigenvalues of this 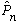, and the eigenvectors.

c) If I have some other arbitrary (but normalized) wave function 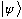, describe as best you can, with words and perhaps integrals the following:

(at a minimum state whether the object is a bra, a ket, an operator, a number, or something else. If you can simplify, or else "intepret"/describe in a physical way, do so.)

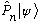i) ? ii) 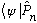? iii) 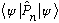? iv) ?

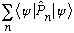5) Operators in quantum mechanics can always be represented by matrices. Sometimes these matrices are infinite dimensional(!), which is a pain, but in many problems we will work with finite matrices after all.

Suppose the operator O can be written as

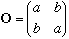
(with "a" and "b" real, nonzero constants)

a) Show that O is Hermitian.

b) Find all the possible eigenvalues, 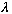, of O, and the corresponding eigenvectors. Please normalize your eigenvectors. (Are the eigenvalues you get real? Should they be?)

c) If this operator represents the Hamiltonian of some system, how many allowed energies does your system have?

Show that the eigenvectors you found in b) are orthogonal.

Show that they also form a complete basis for all 2-D vectors (i.e. all 2 by 1 column vectors)

(F.Y.I, this is the way one would describe e.g. spin 1/2 particles in a magnetic field in quantum mechanics!)