Untitled Document

Course Goals, Physics 3310, Spring 2013

Contents:

What we cover, and why
Course scale learning goals
Chapter by chapter learning goals
Expectations

What we cover, and why: Physics 3310 covers topics in electricity and magnetism (E&M). It is the first semester of your second course in E&M (Physics 1120 was the first), but the first course in a true field theory. Classical electrodynamics (in the form of Maxwell's equations) is one of the most successful physical theories that we presently have. While it is a classical theory (no quantum mechanical Uncertainty Principle here), its conflicts with Newtonian mechanics motivated Einstein's development of Special Relativity. Thus, classical E&M is the first relativistically correct field theory. Also, Maxwell's unification of electricity with magnetism (at first viewed as separate phenomena) was the first and grandest example of unification of forces in physics.

For these reasons, along with the sheer mathematical elegance and completeness of the theory, and its extraordinary (uncanny!) agreement with experiment, electromagnetism is an inspiration for the creation of other physical theories including quantum mechanics and quantum field theory, and indeed much of contemporary physics. Further, classical E&M is at the root of a huge number of practical applications. Most of the phenomena of everyday experience, sights, smells, texture, etc. arise from a balance of electromagnetic interactions and quantum mechanics. E&M is essential in understanding the physics behind electric power generation, electronics, optics, communications, (and on, and on!) We view the universe around us primarily via the electromagnetic radiation. Clearly, to understand the physical world, we need to understand electricity and magnetism!

COURSE SCALE LEARNING GOALS

Math/physics connection: ... translate a physical description of a junior-level electromagnetism problem to a mathematical equation necessary to solve it. ... explain the physical meaning of the formal and/or mathematical formulation of and/or solution to a junior-level electromagnetism problem. ... achieve physical insight through the mathematics of a problem.
Visualize the problem: ... sketch the physical parameters of a problem (e.g., E or B field, distribution of charges, polarization), as appropriate for a particular problem.

Organized knowledge: ... articulate the big ideas from each chapter, section, and/or lecture, thus indicating that they have organized their content knowledge. They should be able to filter this knowledge to access the information that they need to apply to a particular physical problem.

Communication. ... justify and explain their thinking and/or approach to a problem or physical situation, in either written or oral form.

Problem-solving techniques: ... choose and apply the problem-solving technique that is appropriate to a particular problem. This indicates that they have learned the essential features of different problem-solving techniques (eg., separation of variables, method of images, direct integration). They should be able to apply these problem-solving approaches to novel contexts (i.e., to solve problems which do not map directly to those in the book), indicating that they understand the essential features of the technique rather than just the mechanics of its application. They should be able to justify their approach for solving a particular problem.

…a. Approximations: ... recognize when approximations are useful, and use them effectively (eg., when the observer is very far away from or very close to the source). ... indicate how many terms of a series solution must be retained to obtain a solution of a given order.

…b. Symmetries: ... recognize symmetries and be able to take advantage of them in order to choose the appropriate method for solving a problem (eg., when to use Gauss’ Law, when to use separation of variables in a particular coordinate system).

…c. Integration: Given a physical situation, ... write down the required partial differential equation, or line, surface or volume integral, and correctly calculate the answer.

…d. Superposition: Students should recognize that – in a linear system – the solutions may be formed by superposition of components.
Problem-solving strategy: ... draw upon an organized set of content knowledge (LG#3), and apply problem-solving techniques (LG#4) to that knowledge in order to organize and carry out long analyses of physical problems. They should be able to connect the pieces of a problem to reach the final solution. They should recognize that wrong turns are valuable in learning the material, be able to recover from their mistakes, and persist in working to the solution even though they don’t necessarily see the path to the solution when they begin the problem. ... articulate what it is that needs to be solved in a particular problem and know when they have solved it.

Expecting and checking solution: When appropriate for a given problem, ... articulate their expectations for the solution to a problem, such as direction of the field, dependence on coordinate variables, and behavior at large distances. For all problems, ... justify the reasonableness of a solution they have reached, by methods such as checking the symmetry of the solution, looking at limits, relating to cases with known solutions, checking units, dimensional analysis, and/or checking the scale/order of magnitude of the answer.

Intellectual maturity: Students should accept responsibility for their own learning. They should be aware of what they do and don’t understand about physical phenomena and classes of problem. This is evidenced by asking sophisticated, specific questions; being able to articulate where in a problem they experienced difficulty; and take action to move beyond that difficulty.

Maxwell’s Equations. Students should see the various laws in the course as part of the coherent theory of electromagnetism; ie., Maxwell’s equations.

Build on Earlier Material. Students should deepen their understanding of Phys 1120 material. I.e., the course should build on earlier material.

OVERALL COURSE OBJECTIVES:

CALCULATION AND COMPUTATION

Students will be able to:

Compute gradient, divergence, curl, and Laplacian
Evaluate line, surface, and volume integrals
Apply the fundamental theorem for divergences (Gauss’ Theorem) in specific situations
Apply the fundamental theorem for curls (Stoke’s Theorem) in specific situations
Apply Coulomb’s Law and superposition principle to calculate electric field due to a continuous charge distribution (uniformly charged line segment, circular or square loop, sphere, etc.)
Apply Gauss’ Law to compute electric field due to symmetric charge distribution
Calculate electric field from electric potential and vice versa
Compute the potential of a localized charge distribution
Determine the surface charge distribution on a conductor in equilibrium
Use method of images to determine the potential in a region
Solve Laplace’s equation to determine the potential in a region given the potential or charge distribution at the boundary (Cartesian, spherical and cylindrical coordinates)
Use multipole expansion to determine the leading contribution to the potential at large distances from a charge distribution
Calculate the field of a polarized object
Find the location and amount of all bound charges in a dielectric material
Apply Biot-Savart Law and Ampere’s Law to compute magnetic field due to a current distribution
Compute vector potential of a localized current distribution using multipole expansion
Calculate magnetic field from the vector potential
Calculate the field of a magnetized object
Compute the bound surface and volume currents in a magnetized object
Compute magnetization, H field, susceptibility and permeability

CHAPTER SCALE LEARNING GOALS

CHAPTER 1: Vector analysis

TOPICS

Div, grad, curl
Line, surface, volume integrals
Curvilinear coordinates
Dirac delta function
Vector fields (potentials)

PREREQUISITES: Students should already be able to…

Be able to compute correctly div, grad and curl in rectangular coordinates for any test function
Do a path integral along a specific path -- eg. Griffiths 2.20
Be able to expand 1/1+e and 1/1-e when e is very small (Taylor series).

After this course, students should be able to...

... Evaluate the integral from negative infinity to infinity of the delta function, d(x)
... Evaluate the 3-dimensional divergence of 1/r2 in the r-hat direction [4pi delta^3(r)]
... Evaluate the integral of a function times the delta function
... Be able to evaluate the integral of 1/(x-r)^(3/2)dx
... Give a geometrical description of the divergence theorem, and fundamental theorem for curls.
... Change a multidimensional integral in Cartesian coordinates to one in another coordinate system using the Jacobian.

CHAPTER 2: Electrostatics

TOPICS

Electric field, Coulomb’s law
Gauss’ Law, divergence and curl of E
Potential
Poisson & Laplace equation
Work & energy
Conductors

PREREQUISITES: Students should already be able to…

State Gauss’ Law and construct the 3 Gaussian surfaces (sphere, cylinder, pillbox).
Use Cartesian, spherical and cylindrical coordinates appropriately when constructing integrals and surface and volume elements.

After this course, students should be able to...

Electric Field

... state Coulomb’s Law and use it to solve for E above a line of charge, a loop of charge, and a circular disk of charge.
... solve surface and line integrals in curvilinear coordinates (when given the appropriate formulas, as in the inner-front cover of Griffiths).

Divergence and Curl of E; Gauss’ Law

Students should recognize when Gauss’ Law is the appropriate way to solve a problem (by recognizing cases of symmetry; and by recognizing limiting cases, such as being very close to a charged body).
... recognize that E comes out of the Gaussian integral only if it is constant along the Gaussian surface.
... recognize Gauss’ Law in differential form and use it to solve for the charge density rgiven an electric field E.

Electric Potential

... state two ways of calculating the potential (via the charge distribution and via the E-field); indicate which is the appropriate formulation in different situations; and correctly evaluate it via the chosen formulation.
... calculate the electric field of a charge configuration or region of space when given its potential.
... state that potential is force per unit charge, and give a conceptual description of V and its relationship to energy.
... explain why we can define a vector potential V (because the curl of E is zero and E is a conservative field).
... defend the choice of a suitable reference point for evaluating V (generally infinity or zero), and explain why we have the freedom to choose this reference point (because V is arbitrary with respect to a scalar – its slope is important, not its absolute value)

Work & Energy

... calculate the energy stored in a continuous charge distribution when given the appropriate formula
... explain in words what this energy represents.

Conductors

... sketch the induced charge distribution on a conductor placed in an electric field.
... explain what happens to a conductor when it is placed in an electric field, and sketch the E field inside and outside a conducting sphere placed in an electric field.
... explain how conductors shield electric fields, and describe the consequences of this fact in particular physical problems (e.g., conductors with cavities).
... state that conductors are equipotentials, that E=0 inside a conductor, that E is perpendicular to the surface of a conductor (just outside the conductor), and that all charge resides on the surface of a conductor.

CHAPTER 3: Special Techniques

TOPICS:

Laplace’s equation
Boundary conditions and uniqueness
Method of images
Separation of variables in Cartesian and spherical
Multipole expansion

PREREQUISITES: Students should already be able to…

Recognize the wave equation in Cartesian coordinates, and state that eikx is a solution
Recognize the solution to separation of variables in Cartesian coordinates.
Recognize that a function can be expanded in terms of a complete basis, such as sin and cos.
State that conductors are equipotentials.

After this course, students should be able to...

Laplace’s equation

... recognize that the solution to Laplace’s equation is unique.

Method of Images.

... realize when the method of images is applicable and be able to solve simple cases.
... explain the difference between the physical situation (surface charges) and the mathematical setup (image charges).

Separation of variables/boundary value problems

... state the appropriate boundary conditions on V in electrostatics
... recognize where separation of variables is applicable and what coordinate system is appropriate to separate in.
... outline the general steps necessary for solving a problem using separation of variables.
... state what the basis sets are for separation of variables in Cartesian and spherical coordinates (ie., exponentials, sin/cos, and Legendre polynomials.)
... apply the physics and symmetry of a problem to state appropriate boundary conditions.
... solve for the coefficients in the series solution for V, by expanding the potential or charge distribution in terms of special functions and using the completeness/orthogonality of the special functions, and express the final answer as a sum over these coefficients.

Multipole expansions

... explain when and why approximate potentials are useful.
... identify and calculate the lowest-order term in the multipole expansion (i.e., the first non-zero term) for simple charge distributions (generally, monopole or dipole distributions)
... sketch the direction and calculate the dipole moment of a given charge distribution, and use that to calculate the potential and electric field.

CHAPTER 4: Electric Fields in Matter

TOPICS

Polarization & dielectrics
Field of polarized object (bound charges, field inside dielectric)
Electric displacement
Linear dielectrics: Susceptibility, permittivity, dielectric constant
Boundary value problems with dielectrics

Polarization and dielectrics

... go between two representations of dipoles – as point charges, and as generalized dipole vectors – for simple charge configurations.
... calculate the dipole moment of a simple charge distribution.
... name 4 similarities and differences between a conductor and a dielectric (both shield E, conductor shields E completely, dielectric shields via fixed dipoles, conductor shields via mobile electrons).
... predict whether a particular pattern of polarization will result in bound surface and/or volume charge
... explain the physical origin of bound charge.

Field of a polarized object

... sketch the E field inside and outside a dielectric sphere placed in an electric field.
... explain what happens to a dielectric, when it is placed in an electric field.
... explain the difference between free and bound charge.
... identify the appropriate boundary conditions on D given its relationship to E and Qf.

Electric displacement

... sketch the direction of D, P, and E for simple problems involving dielectrics
... calculate the E field inside a dielectric when given epsilon and the free charge on the dielectric.

Linear dielectrics

... articulate the difference between a linear and nonlinear dielectric.
... write down Maxwell’s equations (for electrostatics) in matter, when given the appropriate equations in vacuum.
... state the differences in boundary conditions for fields (D) in matter versus a conductor (D).

CHAPTER 5: Magnetostatics

TOPICS

Currents and charge density
Magnetic fields and forces (Lorentz force law)
Biot-Savart law
Divergence and curl of B (Ampere’s Law)
Magnetic vector potential

PREREQUISITES: Students should already be able to…

Write down Lorentz force law
Know the right-hand rule and how to apply it

After taking this course, students should be able to...

Currents and charge density

... calculate current density J given the current I, and know the units for each.
... explain, in words, what the charge continuity equation 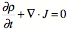means.
... state the vector form of Ohm’s Law () and when it applies.
... calculate the current I, K and J in terms of the velocity of the particle or in terms of each other.

Magnetic fields and forces

... describe the trajectory of a charged particle in a given magnetic field.
... sketch the B field around a current distribution, and explain why any components of the field are zero.
... explain why the magnetic field does no work.

Biot-Savart Law

... state when the Biot-Savart Law applies (magnetostatics; steady currents, dp/dt=0).
... compare similarities and differences between the Biot-Savart law and Coulomb’s Law.
... choose when to use Biot-Savart Law versus Ampere’s Law to calculate B fields, and to complete the calculation in simple cases.

Divergence and curl of B (Ampere’s Law)

... draw appropriate Amperian loops for the cases in which symmetry allows for solution of the B field using Ampere’s Law (ie., infinite wire, infinite plane, infinite solenoid, toroids), and calculate Ienc.
... make comparisons between E and B in Maxwell’s equations (what exactly do we want?)

Magnetic vector potential

... explain why the potential A is a vector for magnetostatics, whereas it’s a scalar (V) in electrostatics. Ie., that the source of magnetic fields is a vector, not a scalar.
Students should recognize that A does not have a physical interpretation similar to V.

CHAPTER 6: Magnetic Fields in Matter

TOPICS

Magnetization – diamagnets, paramagnets, ferromagnets
Field of magnetized object (bound currents)
Auxiliary field H
Linear and nonlinear media: susceptibility, permeability

Magnetization

... calculate the torque or the force on a magnetic dipole in a magnetic field
... explain the difference between para, dia, and ferromagnets, and predict how they will behave in a magnetic field.

The Field of a magnetized object

... predict whether a particular magnetization will result in a bound surface and/or volume current, for simple magnetizations.
... give a physical interpretation of bound surface and volume current, using Stokes’ Theorem.

Auxiliary field H

... calculate H when given B or M
... use H to calculate B when given Jf for an appropriately symmetric current distribution.
... articulate in which physical situations it is useful to use H.
... identify the appropriate boundary conditions on H given its relationship to M and J_free.
... relate M to B to H, given a magnetic susceptibility or permeability.

Important comment on preparation:

Physics 3310 covers material you have seen before (Many of the topics stem from Phys 1120 material) but at a higher level of conceptual and mathematical sophistication.
Therefore you should expect:

a large amount of material covered quickly.
no recitations, and few examples covered in lecture. Most homework problems are not similar to examples from class.
long, hard homework problems that usually cannot be completed by one individual alone.
challenging exams.

Physics 3310 is a challenging, upper-division physics course. Unlike more introductory courses, you are fully responsible for your own learning. In particular, you control the pace of the course by asking questions in class. I tend to speak quickly, and questions are important to slow down the lecture. This means that if you don’t understand something, it is your responsibility to ask questions. Attending class and the homework help sessions gives you an opportunity to ask questions. I am here to help you as much as possible, but I need your questions to know what you don’t understand.

Physics 3310 covers some of the most important physics and mathematical methods in the field. Your reward for the hard work and effort will be learning important and elegant material that you will use over and over as a physics major. Here is what I have experienced, and heard from other faculty teaching upper division physics in the past:

most students reported spending a minimum of 10 hours per week on the homework (!!)
students who didn’t attend the homework help sessions often did poorly in the class.
students reported learning a tremendous amount in this class.

The course topics that we will cover in Physics 3310 are among the greatest intellectual achievements of humans. Don’t be surprised if you have to think hard and work hard to master the material.