 .
.Issued Wed, Mar 4 Due Wed, Mar 11
Required reading for this week: Start Ch. 17
1) Use UNIT analysis to find quick, approximate solutions to the following parts of last week's problems:
#1) 2nd order shift of 1-D H.O. ground state, due to perturbation
 .
.
#2) 2nd order shift of square well, size a, due to pert. +
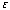 on left, -
on left, -
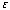 on right
on right
The answers to last weeks problems are (will be) posted, so for credit you must clearly show and explain your work! (Can you argue the signs?)
2) Evaluate the following commutators: a)
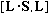 b)
b)
 c)
c)
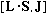
d)
 e)
e)
 f)
f)
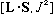 .
.
3) Gas 16-11. (Note 1: Gas. means to use 12-35 and 12-36, not 12-30.)
Note 2: You can (should) solve this problem not just for "low lying" states, but for arbitrary states {nlm}. Eq 12-36 does the necessary integral for you! Please clearly explain why you can use non-degenerate p.t. even for the n>1 levels (which are degenerate.)
4) Gas 16-12. (You don't have to answer the last question, about the E field)
5) Gas 17-5 (see hints, over)
Extra Credit: Gas 16-7. (Ignore the "qualitative explanation" part)
Note: It will help to first find the (normalized) e-vectors and e-values of

Hint for #2) L and S satisfy the usual commutation relations for angular momentum, but they commute with each other. (Also, J = L+S)
Hints for #5 (Gas 17-5):
The eigenfunctions for the ground state of a HO in one dimension are
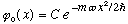 .
.
In 3-D, since the HO potential is separable in x, y, and z, you just multiply together the solutions in x, y, and z! So the ground state in 3-D is just
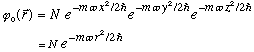
And, the energy eigenvalue is just the sum of the x,y, and z values:
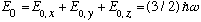
The normalization N is best obtained directly in 3-D. You may use the following facts (which we have seen before!):
Normalization in 3-D:
 .
.
Some useful Gaussian integrals we saw at the beginning of QM I:
 .
.
Finally, don't forget the trick (Gas, p.282 and lecture) that you can rewrite
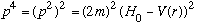 ,
,
where
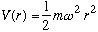 .
.
(Does your final answer have the correct dimensions?)
| 4410 main page | Prof. Pollock's page. | Physics Dep't | Send comments |