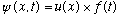Issued Wed, Jan 14 Due Wed, Jan 21

Required reading for this week: Gas. Ch. 14

Here, and throughout the semester, please show your work on all problems. Organize your homework so I can follow your solution clearly. Explain (in words) what you're doing and what assumptions you make, whenever it seems appropriate.

Problems 1-3 are pure review. (Problems 4 and 5 are on some new "spin and matrix related" material.)

1) Write down the usual time-dependent Schrodinger equation for a spinless particle in one dimension with potential energy V(x). Describe how this equation separates; that is, how one can find solutions of the form 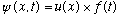. Deduce the form of the function f(t) and the equation that determines u(x). Explain where the energy enters into your discussion.

2) A normalized wave function 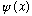can always be expanded in the form 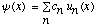, where the functions are a complete orthonormal set of eigenfunctions of the Hamiltonian, with eigenvalues .

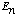a) Explain what all those words mean to you: "complete, orthonormal set", "eigenfunctions of the Hamiltonian", "eigenvalues ".

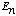(Use equations, or words, as you wish. Be brief! No fancy or technical discussion required, just something simple and explanatory.)

b) Show how it follows from orthonormality that

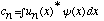
c) Rewrite the eqns 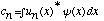and in Dirac notation. (No calculations of any kind required here, I just want you to show me what those equations look like in Dirac notation)

d) Find 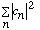. (Show your work! The answer is simple, but where does it come from mathematically?)

e) Explain in words what, e.g., 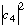tells you.

(How would your answer change if the functions 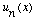were eigenfunctions of some other operator besides energy?)

(over -->)

3) An electron in hydrogen has the following wave fn:

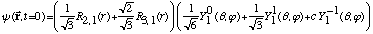
(The 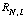's are hydrogen radial wavefns, and 's are spherical harmonics)

a) What must the constant c be, in the expression above? Why? (Is it unique?)

b) If you measure orbital ang. momentum, 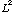, what value(s) might you find, and what is the probability of each?

c) Same, for z-component of orbital angular momentum. Also, what is the expectation value of Lz ?

d) Same, for total energy. Also, what is the expectation value of energy?

e) What is ?

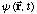f) Suppose you measure Lz and the total energy for the above electron, and you happen to fi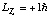nd , and . Write the new wave function, 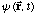after the measurement.

4a) Find the eigenvectors and eigenvalues of

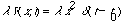
Also, find the inverse of H.

b) Find the eigenvectors and eigenvalues of ,

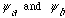where 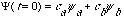is just some given constant.

Also, find the inverse of H.

5) Gas 14-1.