Issued Wed, Apr 8 Due Wed, Apr 15

Required reading for this week: Ch. 13 (and Ch. 19 for fun. You can skip the section on the Hartree approximation, just read about the periodic table)

1) In class (notes, p. 185) we will derive the variational estimate for the ground state energy, E, of the molecule as a function of R (the inter-proton distance). This is Gas. Fig 20-2, and eq. 20-14 (except I claim he has some mistakes in that formula. My notes, and Griffiths Eq. 7.51 get it right.)

i) Plot E versus R, and reproduce the lower solid curve of Gas. Fig 20-2.

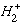ii) (This is basically Griffiths' 7.10) The 2nd derivative of the curve above can be used to estimate the natural frequency of vibration ( ) of the molecule.

a) Explain clearly how to relate the 2nd derivative to vibrational energies.

b) Use part a to make a rough estimate of how many bound vibrational levels there are for .

Note: You'll want to find the minimum, and the second derivative at that point, numerically rather than analytically!

2) Atomic states are often described in spectroscopic notation, Gas Eq.15-52. E.g., the ground state of He is , (The angular momenta in that notation, , arise from summing up over all the electrons.)

i) List all possible spectroscopic states in Helium, , that can arise if the electrons have a total, combined orbital angular momenum of L=2.

Which of these states are allowed by Pauli?

ii) The ground state of silicon has electrons filling all the n=1 and n=2 levels. (these all pair up to yield an "inert core" with no net spin or angular momentum of any kind). On top of this core, Si has 2 electrons filling the 3s level (again, paired up with zero net spin) and finally 2 last electrons that go into the 3p level.

a) How many electrons does this add up to? (Check: = atomic number for Si?)

b) List all possible spectroscopic states for the ground state of the Si atom which satisfy the Pauli Principle. (over ->)c) One of Hund's rules says the state of highest spin will have the lowest energy. Which of the states you listed above remain, by this rule?

d) Another of Hund's rules says, given this spin, the state of lowest total angular momentum will have the lowest energy. What, then, is the spectroscopic notation for the ground state of Si?

(As you can see, the arguments for silicon are very similar to those for carbon, and indeed their chemistry is similar. This is what led the original Star Trek writers to introduce "silicon-based life forms" in an early episode)

3) The Hamiltonian for an electron in the presence of electromagnetic fields is

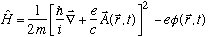
(NB: I think Gas has the sign wrong on the potential term throughout Ch. 13)

i) Show that, in any state, .

(In other words, "m v" is not equal to "p" in QM with E+M fields!)

ii) Verify/show the mathematical relation I use in my notes:

,

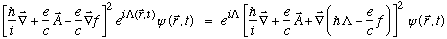where are arbitrary scalar functions of space and time.

4) Gas. 13-7. All I really want is the most general form of the allowed energies, you don't have to solve for the eigenfunctions.

Can you give a very simple classical picture of the motion?

Hint: This problem may seem pretty tough at first. It will help a lot if you can find an A field that satisfies 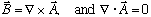, and also such that A only has a y component. (That's what Gas meant by his hint).

Gas, on p. 226, has worked through a very similar problem. He is missing the E field, but this makes only a fairly minor modification. His procedure on that page is a fine way to get started. In the end, the Schrodinger equation separates in Cartesian coordinates, and the 3 separate equations in x, y, and z are all familiar old equations whose solutions you can write down by inspection...