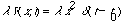Issued Wed, Apr 22 Due Wed, Apr 29

Required reading for this week: Ch. 21

Final Exam is Fri, May 8, 7:30-10:30

1a) Gas 21-3 (See hints)

b) The complete answer to part a is a bit messy, and hard to think about. There is one thing you can pull out relatively easily without doing all the "complex squaring" algebra: at what frequency, f, does the system go haywire? (i.e., what frequency f makes it really want to make transitions!)

c) Suppose instead your pertubation were 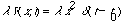. What is now the probability that you will find the particle in the nth state after a long time? (This should be somewhat easier.)

2) Gas 21-7 (See hints!)

3) Suppose you have an original (unperturbed) Hamiltonian, H0, that has only 2 linearly independent eigenstates, 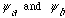. At t=0 you start off in a state 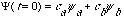. At t=0, the Hamiltonian is now modified by an additional extra potential term, V(x,t) . So, as in class, you can write the time dependence after t=0 in the completely general form: .

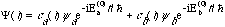For simplicity, assume that ("Diagonal matrix elements of the perturbation vanish" - there are lots of physics problems where this occurs).

i) Find a pair of (coupled) differential equations for the time derivatives of 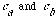. (This is basically asking you to rederive a direct analogy of Gas. 21-9 here, but do not make any approximations about V(t) being small - for this two level system, your formulas are exact!)

ii) Suppose (a constant, independent of time). Suppose you started off in state "a" at time 0. What is the probability of being in state "a" at time t? How about state "b"? (Do your probabilities add up to 1? Should they?)

iii) The probability of transition, in part ii should come out sinusoidal in time. What is the frequency, f, of this sin wave? Your answer, remember, is exact! How does it compare with the approximate answer we obtained using TDPT? (i.e., the frequency from Gas Eq's 21-17 and 21-18, in the special case we have here, namely from Eq. 21-11 is zero.)

Hint for #1) You should only work to first order in perturbation theory. Do not include any terms, anywhere, that are manifestly of order (something small)^2.

Another hint for #1) You should work out the time integral explicitly, and be very clear about what you need to do to get the final answer. But, at a certain point, when you have a slightly ugly complex expression which you need to (absolute value) square to get the probability of transition, don't bother squaring it out. (It won't simplify) You should, however, put all your terms over a common denominator - this will tell you the answer to part b immediately.

Hint for #2) This would be a rather difficult problem, if not for the fact that Gas. has done it in great detail for hydrogen. His final rsult is givein in Eq. 21-104. What is different for the harmonic oscillator? Not a whole lot - the radial wavefunctions are different, so the radial integral in Eq. 21-95 has to be re-done. Note, for the harmonic oscillator in 3-D:

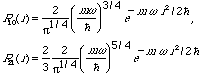
There's one other correction to make. The energy difference between the n=1 and n=2 levels enters into the final result, and is of course not the same for the harmonic oscillator as it was for hydrogen. Look carefully through the calculations done by Gas for hydrogen, (summarized in Gas Eq. 21-98, and 99) and figure out exactly how the energy difference enters, and you can simply correct for it (It's a multiplicative constant in both cases, just a different constant).

I claim there's nothing else different - all the angular stuff, polarization, everything else is identical. So, you don't have to redo the calculation at all - you can just take Gas' answer (Eq. 21-104) and simply "fix it up" by correcting for the new radial integral and the different factors...