 ,
when it's initially in the particular (special) states
,
when it's initially in the particular (special) states
 and also
and also
 .
.
Issued Wed, Jan 28 Due Wed, Feb 4
Required reading for this week: Finish Gas. Ch. 14, Start Gas. Ch. 15
1) In my class notes (pp 40-41 ) I derive the time evolution of the state of a
particle precessing in a magnetic field
 ,
when it's initially in the particular (special) states
,
when it's initially in the particular (special) states
 and also
and also
 .
.
a) Find <S_x>, <S_y>, and <S_z> (expectation values of the
three components of spin) if the particle is initially in the state

b) If you measure S_x (once) at time t, what is the probability you will get +
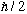 ?
Same question for S_y and S_z.
?
Same question for S_y and S_z.
c) Try to sketch, crudely/classically (or just describe in some intuitive way) how you picture the behaviour from part a. (Can you somehow try to draw a "classical picture" of S as a function of time?)
2) Below, I will refer to an "n"-SG, which means a Stern-Gerlach device
measuring spin in the n direction (i.e. measuring
 ).
).
So, e.g., a "z"-SG measures
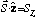 ,
it's just a usual SG device measuring z component of spin.
,
it's just a usual SG device measuring z component of spin.
The result of running spin 1/2 particles through an "n"-SG is always two
separated beams, which you could call
 and
and
 ,
having
,
having
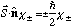 .
.
(i.e. the output beams are "up" and "down" in the n direction)
For all parts below, you will be asked to answer two questions:
i) what is the quantum state of the output beam?
(give it in the form
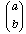 ,
you just tell me what a and b are), and
,
you just tell me what a and b are), and
ii) How many particles/sec are in the output beam?
The initial beam has
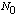 particles/sec, all in the initial state
particles/sec, all in the initial state
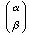 .
.
(Problem continues on other side ->)a) The beam runs through a
"z"-SG, but I block off the output beam with eigenvalue -
 .
So only the +
.
So only the +
 beam is output. (Answer i and ii above.)
beam is output. (Answer i and ii above.)
b) Take the resulting beam from part a, and run it through an "x"-SG.
Again, block the -
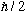 beam, so only the +
beam, so only the +
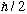 beam is output. (Answer i and ii.)
beam is output. (Answer i and ii.)
c) Take the resulting beam from part b, and run it through a "z"-SG
again. As usual, block off the -
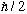 beam. (Answer i and ii.)
beam. (Answer i and ii.)
d) Now take the resulting beam from part c, and run it through an
"n"-SG, where n is in the direction
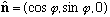 .
(Again, block off -
.
(Again, block off -
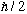 )
(Answer i and ii.) Note for d: feel free to use the results Gas. derived on
p. 243 and 244, especially Eq. 14-56.
)
(Answer i and ii.) Note for d: feel free to use the results Gas. derived on
p. 243 and 244, especially Eq. 14-56.
3) Gas 14-14.
(This one is probably the hardest on this problem set. Be careful with your algebra, especially when you have to square sums of complex numbers!)
4) Gas 14-15.
Note! Gas asked you to find
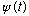 for three different cases! (i.e, with initial state the eigenstate of
for three different cases! (i.e, with initial state the eigenstate of
 for all three eigenvalues
for all three eigenvalues
 .)
.)
But, I only want you to do the single case where the initial state is the
eigenstate of
 with eigenvalue 0. Don't forget to normalize your wavefunctions...
with eigenvalue 0. Don't forget to normalize your wavefunctions...
________________________________________________________________
The last question is not for credit (so don't turn it in), but if you want to understand paramagnetic resonance, I recommend you do it:
Solve the equation
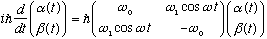
for
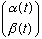 ,
with
,
with
 given constants, and
given constants, and
 .
.
Show explicitly that
 ,
,
where
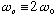
(This is precisely what I did in my notes, pp. 48-50. I skipped a few steps, which I want you to fill in. Even for the steps I did show, try to derive it all yourself. Just use my notes to help guide you if you get stuck...)
| 4410 main page | Prof. Pollock's page. | Physics Dep't | Send comments |