Physics 4410, Spring '98 Extra
exercises
This is not due, it's just for your own practice, if you want to
understand the last part of Ch. 15 better.
(I'll put solutions in the library)
1) Gas 15-3.
Note: Write your results in the notation of Eq. 15-52. E.g, one possible state
is
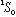 .
The upper 1 tells you 2
.
The upper 1 tells you 2
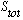 +1=1,
i.e.
+1=1,
i.e.
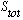 =0,
where
=0,
where
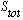 is the total spin state of the system. The big explicit letter S tells you that
you're in an "orbital S state", which means L=0. The lower 0 tells you what
total J is. So this is the "spectroscopic" notation for the state
is the total spin state of the system. The big explicit letter S tells you that
you're in an "orbital S state", which means L=0. The lower 0 tells you what
total J is. So this is the "spectroscopic" notation for the state
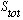 =0,
L=0, J=0.
=0,
L=0, J=0.
It turns out there are infinitely many such answers. List at least all the
possible L=0 states (i.e. with a big letter S) and all the possible P states,
and perhaps say in words what patterns you see. Don't forget the Pauli
principle: two identical spin one objects must be in an overall state which is
symmetric under interchange!
2)15-6
3) 15-7 (Assume there is no L in this problem, i.e. L=0)
If you want more practice with addition of angular momentum, here's a couple:
i) Two electrons are each in a "p orbit". The total 2-electron system has
total angular momentum 1, with total z component -1. If you
measure the z component of spin of electron number 1, what values may be found,
with what probabilities? (Neglect spin entirely in this problem)
ii) If you have 3 electrons, all in p states, what are the possible values of
total angular momentum? (Again, neglect spin entirely)
iii) How many independent eigenstates are there for a system of two particles,
one with spin 3 and one with spin 1?
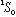 .
The upper 1 tells you 2
.
The upper 1 tells you 2
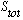 +1=1,
i.e.
+1=1,
i.e.
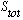 =0,
where
=0,
where
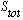 is the total spin state of the system. The big explicit letter S tells you that
you're in an "orbital S state", which means L=0. The lower 0 tells you what
total J is. So this is the "spectroscopic" notation for the state
is the total spin state of the system. The big explicit letter S tells you that
you're in an "orbital S state", which means L=0. The lower 0 tells you what
total J is. So this is the "spectroscopic" notation for the state
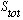 =0,
L=0, J=0.
=0,
L=0, J=0.