Issued Wed, Feb 18 Due Wed, Feb 25

Required reading for this week: Gas. Ch. 16.

(You might want to look at Griffith's chapter on perturbation theory, too.)

1) Gas 15-5 (Write your answers in "spectroscopic notation", a la Gas. 15-52)

Hint: I get exactly 6 possible answers, but only 4 of those are possible if the pion has negative parity.

2) The Hamiltonian of a spin system is given by

. (Neglect orbital angular momentum, L=0).

Find the eigenvalues and eigenfunctions of the system if the two particles are identical spin 1 particles. (Don't forget the Pauli principle, which says identical bosons must be in a totally symmetric state)

(This is sort of like Gas 15-7, one of the "optional problems" from last week)

___________________________________________________________________

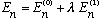We may or may not get far enough in lecture to fully derive this, but for the rest of this homework all you need is Gas 16-7 and 16-12: the energies of a system with are , where

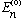= the energy eigenvalues of 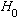, (with corresponding e-fn ,)

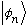and the correction term is .

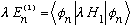3) Last semester (HW 7) you solved (exactly) for the energies and eigenvectors of a particle in a square well with a delta function in the middle:

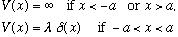
Now you will treat this problem as a perturbation: will be the usual square well (from -a to +a), and the perturbation is then just

Find the energies , using first order perturbation theory.

(Why are the energies unperturbed for even n?) (over ->)

4) For a harmonic oscillator, , and we know , with 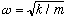. Now suppose k is slightly increased, i.e. .

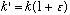(Imagine the spring has been slightly cooled, to make it "stiffer".)

a) Find the exact energies of the new system. (This is a "quicky", just write it down!) Expand your answer as a power series in .

b) Now calculate the energies using first order perturbation theory, and compare with part a. (What exactly is here?)

(Note: no integrals need to be calculated for this problem, if you remember the virial theorem, <K.E.> = <V> for a harmonic oscillator)

5) Gas. 16-2, but just do the n=1, l=0 state (i.e. ground state) only.

Hint: If