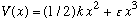Issued Wed, Feb 25 Due Wed, Mar 4

Required reading for this week: Finish Gas. Ch. 16.

Pick any 4 of these problems. Turn in only four! (If you do them all, give the one you feel you did worst on to me separately for extra credit)

1) Real systems often look "locally" (near x=0) like a harmonic oscillator, but have some small deviations at larger x that is called an "anharmonic perturbation": 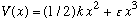. Show that the shift of all the energy levels of the harmonic oscillator, due to first order perturbation theory (PT) using this potential, vanishes.

Then use 2nd order PT to estimate the shift in just the ground state energy.

2) The bottom of an infinite square well is modified so that it is shifted up by 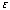on the left half, and down by 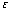on the right half. Do as in the previous problem: show that the first order PT corrections to all energy levels vanish, and find the 2nd order PT corrections to the ground state energy.

3) Gas 16-10a

4) Gas 16-9. Just do the energy shift for ground and (degenerate) first excited states, and 2nd order energy shift for ground state. You do not have to "interpret", or "solve the problem exactly" (though it's fun to try!)

5) Suppose we have an "infinite cubical well" of size a:

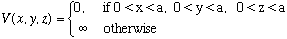
Now perturb this potential with a small delta function bump at the point (a/4, a/2, 3a/4):

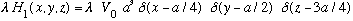
(Where 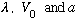are all just given constants)

a) Find the first order correction to the energy of the ground state.

b) Find the first order correction(s) to the energy(ies) of the (triply degenerate) first excited state(s).

Show the results for parts a and b by a little "energy level sketch" (like fig16-1 in Gasiorowicz) Find the particular linear combination(s) of

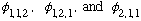that correspond(s) to the energy level(s) of part b that shift upwards.

A few hints for this homework:

1 The first part is quick and simple (use symmetry!) For the 2nd order PT,

all you need is the expectation value of x^3 between harmonic oscillator states. To work this out is a little hard but doable - first use "completeness", i.e use the trick 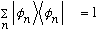TWICE:

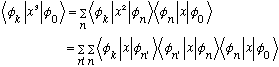
The matrix elements of x you need above you can find using Gas 7-4, i.e. writing x in terms of A and 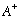. You did this last semester in Problem 7-3. Remember:

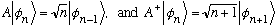
(At first it looks like you need a "double infinity" of matrix elements, but by orthonormality of 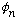's, those matrix elements are almost all zero!!

My final answer comes out to be 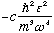, (where c is a ratio of integers that comes out a bit more than 1) If you do it right, you'll find c exactly.

Note the sign! As discussed in class, it must come out negative.

2) I needed MMA to compute a sum I couldn't figure out analytically.

3) Many of the tricks regarding A and Adagger from #1 are used here too.

4) You must use degenerate perturbation theory for the 1st excited state(s).

5) This is Griffith's problem 6.8. He does an example problem (p. 231-234) that's pretty similar to this one. (If anything, the delta functions make doing any required integrals easier than the example he worked out.)

You solved for the eigenfunctions and eigenvalues of the unperturbed 3-D infinite box last semester. If you forget how it went: write out Schrodingers equation in 3-D Cartesian coordinates, and try separation into X(x)Y(y)Z(z). You'll find you have 3 independent x, y, and z infinite square wells. The 3-D eigenfunctions are just this product of familiar 1-D wavefunctions .

The energies are .

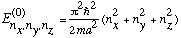The ground state 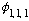has energy 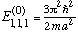. (nondegenerate)

The first excited state is triply degenerate, .

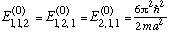(This part of the problem is an excercise in degenerate perturbation theory.)