Physics 4410 2nd Exam (1 1/2 hours) Apr 2, 1998
Your name:
Please read these directions BEFORE beginning.
As always, please show all your work, and explain reasoning clearly where necessary.
You may have a normal 8.5 x11 sheet of paper with your own notes, written on one side only please.
The problems are not of equal value.
You must do problems 1 and 2, but problems 3 and 4 each give you a choice of doing either part a, or part b. (Do not do both parts, pick one)
Feel free to look over my crib sheet before the exam begins. Don't hesitate to ask me if you have any questions!
Time dependent Schrodinger eqn:
Time independent Schrodinger eqn:
The spin operator (for spin 1/2) is
Some spherical harmonics:
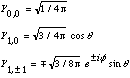
First order non-degenerate PT:
2nd order non-degenerate PT:
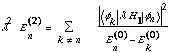
First order degenerate PT: If you have states
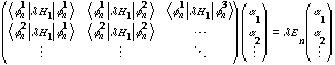 ,
,
(These eigenvectors tell you the linear combination of the
Hydrogen atom fine structure formulas:
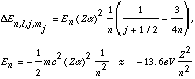
Bohr radius (and fine structure constant):
1) A particle, mass m, is in a one dimensional box with walls at x=-a and +a. A small perturbation is added,
a) Briefly discuss (no calculations required!) the effect of H' on the ground state. (Discuss the effects on both the energy and the wave function.) (6 pts)
b) Use unit analysis to estimate the leading (nonzero) correction to the energy of the ground state. (10 pts)
c) Very roughly, how big would
2) A quantum system with 3 linearly independent states,
a) Find the eigenvectors and eigenvalues of the unperturbed system, i.e. when
b) Solve for the exact eigenvalues of H. (Hint: The matrix is block diagonal)
Then give the sol'ns as power series in
c) Write explicitly what the perturbation
Then use first and second order nondegenerate perturbation theory to find the approximate energy eigenvalue for the ground state. (Check if your answer in b was correct) (8 pts)
d) Use first order degenerate perturbation theory to find the approximate energy eigenvalues for the initially degenerate first excited states. (Again, compare with part b: discuss briefly.) (6 pts)
e) What are the new eigenstates after turning on the perturbation, (i.e. including nonzero
in terms of
CHOOSE one of the following two lettered parts, i.e. EITHER do 3a or 3b, please do not do both!
EITHER: 3a) State carefully, in your own words, the handy theorem we used so often in class to justify the use of non-degenerate perturbation theory even when there were in fact degeneracies. Then, prove the theorem. (24 pts)
OR: 3b) Briefly discuss (perhaps a short paragraph each) all four of the following: (24 pts total)
i) Level repulsion
ii) 21 cm line
iii) Fine structure
iv) Lamb shift
CHOOSE one of the following two lettered parts, i.e. EITHER do 4a or 4b, please do not do both!
EITHER 4a) As we learned in class, the ground state of hydrogen is split into two levels by the hyperfine interaction:
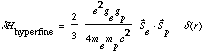 .
.
Recall, the ground state of hydrogen has a spatial wave function
where a0 is the Bohr radius.
i) Derive the resulting hyperfine energy splittings, and sketch an energy level diagram (clearly labelling states and energies). Please show your work, and explain clearly. You do not have to plug in any numbers, a symbolic answer is fine. (12 pts)
ii) Now put hydrogen, in its ground state, into a strong magnetic field. Discuss what happens. Sketch an energy level diagram, clearly labelling states and energies. (8 pts)
Hint for ii
: the energy of a spin 1/2 particle in a magnetic field isHere, both the proton and the electron will gain such an energy, and these energies simply add...
A strong field means the hyperfine splitting can be neglected. (g is 5.6 for a proton.)
OR 4b) A hydrogen atom is in a state with n=2, and
Sketch an energy level diagram for these two states, clearly labelling states and energies .
How does your sketch change if I remind you the relevant radial integral comes out negative?
(In this problem, please show all your work clearly - don't just quote Stark results.) (15 pts)
ii) Repeat part i if the electric field is in the +x direction. (5 pts)
Your name ____________ Problem number for this page ______