As always, show all your work, and explain reasoning clearly where necessary.

You may have both crib sheets from previous exams, plus one extra 8.5 x11 sheet of paper with your own notes

The 6 numbered problems are all of equal value (15 pts each total, for an exam total of 90 pts) The sub-parts, however, are not all of equal value.

Feel free to look over my crib sheet before the exam begins. Don't hesitate to ask me if you have any questions!

Time dep’t Schrod. eqn: . Time independent Schrod. eqn:

Hydrogenic atoms have energies

Particle in a box:

Pauli spin matrices: ,

(All have the same two eigenvalues, )

The eigenvectors of are . The eigenvectors of are .

Total angular momentum J=L+S. Spectroscopic notation is written as

Notation for eigenfunctions of angular momentum:

First order non-degenerate PT:

2nd order non-degenerate PT:

Time-Dependent PT: If V(t) is added, starting at t=0, to a system initially in state k, then the probability of making a transition to state m after time t is given by the absolute square of

Variational theorem: Given a Hamiltonian H, and any arbitrary normalized wavefn ,

then the ground state energy of H satisfies

Gauge transformations are characterized by a function f(r,t):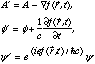

EM fields in terms of potentials:

1) A particle is initially in the ground state of a 1-D infinite square well (running from x= 0 to a.) At time t=0, a brick is dropped into the well so that the potential suddenly becomes

(The potential is, of course, still infinite elsewhere).

At time T the brick is quickly removed, and the energy of the electron is measured. What is the probability the energy is now (the first excited state energy)? (15 pts)

2) An electron in an EM field has a Hamiltonian , with .

a) What is the electromagnetic field configuration this electron is sitting in? (Use words, as well as an equation, to describe the E and B fields.) (3 pts)

b) Expand this Hamiltonian out explicitly to get a resulting Schrodinger equation in Cartesian coordinates that we could solve with familiar methods. (But, do not try to solve it!)

(Hint: Your result should have 3 pieces, one independent of , one linear in , and one quadratic in . The part linear in should look like . But, what is the right overall sign? And, what is the correct numerical coefficient? (1? 2? 1/2? Factors of 2 matter!)

Please show your work carefully, don’t just write down an answer. (5 pts)

c) Suppose that we solved part b, and called that solution . Now I pick a different gauge; I will choose (the third component has changed) and there is still no scalar potential in the problem.

i) Show that this new ( "primed") gauge is physically equivalent to the original one. (2 pts)

ii) Find the new wave fn in the new gauge, in terms of the old wave fn ?(3 pts)

iii) Note that . Does this cause any problems for us? (Is it allowed?) (2 pts)

3) A particle, mass m, in 1-D sits in the potential

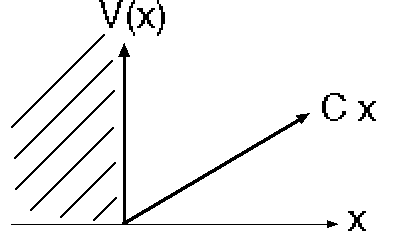
(This potential is what a small object sitting on a table feels, due to gravity! It can’t go below the table (x<0); and above it, the potential energy simply grows linearly with height)

a) Use the variational method to estimate the ground state energy. (13 pts)

For your trial wavefunction, choose

b) Check that your answer has correct units! (2 pts)

What total angular momentum values J are permitted for a system (e.g, a complicated atom) with total ground state wave fn designated in spectroscopic notation as ? ? ? (3 pts)

b) Which of the following could, in principle, be a total state of 2 identical particles?

Note: For those that are not possible, please state clearly why not... (6 pts total)

2 electrons in a state? 2 electrons in a state?

2 spin-1 particles in a state? 2 spin-1 particles in a state?

c) Boron (Z=5) has a structure. What are the possible spectroscopic notations for the ground state? (3 pts)

d) Helium’s ground state has an energy of -79.0 eV. What is the energy required to completely remove one electron? (3 pts)

5) Briefly discuss (perhaps a couple of sentences each) any 5 of the following: (3 pts each)

a) 21 cm line

b) Aharanov-Bohm effect

c) Exchange energy (or "exchange interaction") in Helium

d) Linear combination of atomic orbitals (LCAO) method

e) EPR paradox

f) Ortho- and para-helium

g) Gauge invariance in quantum mechanics

h) Selection rules

6) A spin particle in a uniform B field (in the z direction) has (with "a" some positive, real, given constant.)

a) What are the unperturbed energy eigenvalues? (Call them and , with being the lowest energy, i.e. the ground state. Call the corresponding eigenvectors and ) (2 pts)

b) Suppose the system in part a is modified by the addition of a perturbation (i.e. there’s also a B field in the x direction.) "c" is some positive, real, given constant.

i) Solve exactly for the energy eigenvalues. (Make no assumption about c being small) (2 pts)

ii) Assuming c is small, use perturbation theory (you will need to go out to second order!) to estimate the ground state energy of the perturbed system. Compare with part i. (4 pts)

iii) Again without assuming c is small, use the variational method to estimate the energy of the ground state. Use a trial wave fn of the form , where is your variational parameter. (Recall, must be normalized to use the variational method. Do show that is automatically normalized.) (Note: Once you find a formula for , you’re nearly done. If you’re running short on time, don’t bother plugging it back into your expression to actually work out the energy. Part iv tells what you’ll get! It’s only worth 1 pt...) (5 pts)

iv) The variational answer and the exact answer agree perfectly. Explain (briefly) why this happens. (Note: You can answer this even if you didn’t get any of the above parts...) (2 pts)