Here's a long extra credit problem. I have designed it as a series of "show that's", so if you can't get one part, you can always still go on. If you do this problem, please turn it in to me separately. The problem is essentially the physics of NMR (nuclear magnetic resonance), also called MRI (magnetic resonance imagining).

Consider an electron placed in an external magnetic field with a large constant z component , and a much smaller time varying x component .

The full time dependent Schrod. Eqn reads , where is the time dependent "wave function" (or, "spinor") of the electron.

a) Use Griff. Eq 4.158 to show that

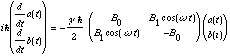
(Remember, is a known constant of nature)

b) Make some definitions to cut down on the symbols you have to keep writing:

. Also, let's define related functions (this is not such an obvious step, but you'll see shortly that it turns out the just be a clever trick to help make the problem easier to solve)

Plug all these redefinitions back into the diff eq. of part a, to find the diff eq's that A(t) and B(t) solve, namely show that

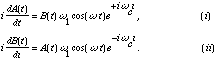
c)In expression (i) above, you could rewrite .

(do you see this?) Remember, is the time dependence of the small external x component of the magnetic field; you can TUNE it so that it is very close to . In this case, I claim the term oscillates like mad with time, and averages away to zero. So, you can simply throw it out (!!) Do this, and do the same for equation (ii ) (it'll look slightly different because of the different sign in the exponent, but throw away the one term that oscillates like crazy). After you do this, take equation (i) and use it to solve for B(t), and plug this into equation (ii). Show that this results in the equation

d) We need to solve the above diff eq. It's not hard. As a trial guess, let , plug it in, and show that the general solution for A is ,

where , and are (as yet undetermined) constants.

Also, once you know A(t), eq. (i) in part b above (with that approximation you made in part c) should allow you to immediately see

. (Verify this)

To finish up this part, just use your original definitions of A(t) and B(t) to find what you really want, which is a(t) and b(t).

e) Now let the electron at t=0 point in the +z direction, i.e. let .

This is a "boundary condition" that will allow you to determine the constants . Now use these to find |b(t)|^2 .

Take the limit that . Show that in this case,

DISCUSSION: What did you just discover? The spins in the sample were originally lined up in the +z direction: this is what tends to happen naturally with electrons in a strong B field, they're like little magnets and they prefer to line up. But then you add a small, time varying x component. You tune the time variation frequency until it matches a natural frequency of the problem, . (Which is the Larmor frequency, it's the natural frequency at which the electrons tend to "precess" around the z axis) At this point, you discovered |b(t)|^2 (which is the probability that the electron would be found spin down) oscillates like crazy, regularly becoming as large as 1. At such a time, the electrons in your sample have all flipped upside down, which requires a large (fixed) amount of energy! By measuring the size of this energy absorption of your sample, you basically detect how many electrons flipped, i.e. the density of your sample, which is what you're after. This is (rouhgly) the basic physics behind MRI devices in hospitals, e.g. (Measuring the resonant frequency itself tells you about the character of the sample, because it depends on , the gyromagnetic constant. This is the basis of "paramagnetic resonance imaging" of crystals...)