i) ``p orbit" means l=1. Adding l=1 and l=1 to get
Solutions to extra problems associated with Clebsch-Gordon tables. (Don't bother looking at these solutions without really trying the problems first - at least, I claim it won't do you any good!)
i) ``p orbit" means l=1. Adding l=1 and l=1 to get
![]() means
we have to go to the C-G 1x1 table, and read down the
means
we have to go to the C-G 1x1 table, and read down the
![]() column.
column.
| (1) |
So there's a 50% chance of m1=0, and a 50% chance of m1=-1.
ii) We're adding l=1 and l=1 and l=1. The first pair of them will add up to something we might call the ``total angular momentum of the first two", which in turn we might label l1 2. There are three possibilities for l1 2. It is 1+1 = 0, 1, or 2. Now, the grand total is the quantum sum of l1 2 and the remaining, third angular momentum, namely 1.
If l1 2 is 0, you get ltot= l12 +1= 0+1 = 1.
If l1 2 is 1, you get ltot = l12+1 = 1 + 1 = 0, 1 or 2.
If l1 2 is 2, you get ltot = l12+1 = 2 + 1 = 1, 2, or 3.
Putting all this together, I see that we can get a final, total angular momentum of 0, 1, 2, or 3. (1 can be built in several ways, 2 can be built two different ways, 0 and 3 can each be built only one way)
iii) Spin 3 has 2*3+1=7 possible states. Spin 1 has 1*1+1=3 states. The combined system can have 7*3=21 possible basis states.
iv) 1+2 = 1, 2, or 3.
a) We are given the total state is
![]() .
So go to the 2x1 C-G table, and read down the
.
So go to the 2x1 C-G table, and read down the
![]() column. This gives the answers directly. If you're measuring the
z-component of the spin two particle, focus on the first entry in the
row names:
column. This gives the answers directly. If you're measuring the
z-component of the spin two particle, focus on the first entry in the
row names:
3/5 chance of +2, 3/10 chance of +1, and 1/10 chance of +0.
iv-b) Now we're given the microscopic state, so we must
read across. We're still in the 2x1 table, and we read acros the row
corresponding to
![]() (which of course in the table
is simply given by the m components, i.e. it's labelled -1 -1.
Reading across, I see our state is
(which of course in the table
is simply given by the m components, i.e. it's labelled -1 -1.
Reading across, I see our state is
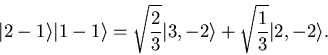 |
(2) |
By the way, the order doesn't matter. S2 and Sz commute, so measuring one won't mess up the other.
v) In all these questions, we will use
Stot=S1+S2, which
means
| (3) |
a) We're adding spin 1 (So
![]() )
and spin 1/2 (So S22= 3/4
)
and spin 1/2 (So S22= 3/4![]() ). Stot can clearly be 3/2 or 1/2 here. We're told
we're getting Stot=1/2, and mtot=1/2, so
). Stot can clearly be 3/2 or 1/2 here. We're told
we're getting Stot=1/2, and mtot=1/2, so
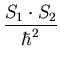 |
= | (4) | |
| = | (5) |
This gives us an energy of H = A + B(-1)+C*mtot = A-B+C/2.
b) Now S1=S2=1/2, so Stot = 0 or 1. We're told
Stot=1, and mtot=0. So
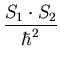 |
= | (6) | |
| = | (7) |
This gives us an energy of H = A + B/4 +C*mtot = A+B/4.
c) If the particles are identical and spin 1/2, Pauli says they must be in an
antisymmetric state. Since spin is all we have to work with here, they must
be in the antisymmetric spin state, which is the Stot=0 one.
(And of course, if S=0, mtot=0 is required as well) So we have
 |
= | (8) | |
| = | (9) |
This gives us an energy of H = A - 3B/4 +C*mtot = A-3B/4.