2i) A particle of spin 1 moves in Hamiltonian of the form

. (A, B, C, D are given constants, with units of energy)

Suppose the particle has a known orbital ang. momentum L, and define J=L+S, as usual.

a) What would the value of energy be, in the state where J=L+1?

b) How about the state where J=L?

(Your answers should involve the constants A, B, C, D, and L, only)

2ii) Show that in general .

3i) A 3He nucleus is made of 2 protons and a neutron. In the ground state, all the particles are at rest relative to one another. (Thus, there is no orbital angular momentum between any of the particles) What possible eigenvalues of total angular momentum squared, , can the 3He nucleus have, if you ignore the Pauli principle?

(Note: protons and neutrons are spin 1/2 particles)

3ii) How does the Pauli principle change your answer?

(A cool result - you can deduce the spin of 3He in this way, with no ambiguity!)

4) A particle with spin 1 is put into an orbit with orbital angular momentum L=1.

As usual, the total angular momentum is the sum of spin and orbital, J=L+S.

My notation for the three possible spin orientations of a spin 1 particle is:

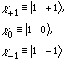
For the remaining questions, put this particle into the following total quantum state:

.

i) If you measure , what value(s) can you get, with what probabilities?

Same question, for .

(over ->)

ii) Suppose instead you measure , the z component of spin only. What values can you get, with what probabilities?

iii) Imagine you measure , and you happen to get . *After* that measurement, you go ahead and measure . What values can you get, with what probabilities?

iv) Based on your answers above, do you think and commute? Explain briefly.

(No calculation is required)

5) Throughout this question, SG stands for a "Stern-Gerlach device", which measures some particular component of spin. (E.g., a "z"-SG measures the z component of spin - see Griffiths 4.4.2 if you want more details about how SG devices actually work.)

You begin with an incoming beam of electrons (all spin 1/2), with a flow of electrons/sec, all of them in the exact same initial quantum state ,

where , and are some given constants.

______________________

For each lettered part below, you will be asked to answer two questions:

i) what is the quantum state of the output beam?

(give it in the form , just tell me what a and b are), and

ii) How many particles/sec are in the output beam?

______________________

a) The beam runs through a "z"-SG, but I block off the output beam with eigenvalue

-. So only the + beam is output. (Answer i and ii above.)

b) Take the resulting output beam from part a, and run it through an "x"-SG. Again, block the - beam, so only the + beam is output. (Answer i and ii.)

c) Take the resulting output beam from part b, and run it through a "z"-SG again. As usual, block off the - beam. (Answer i and ii.)

6i) Griffiths 6.1

6ii) Griffiths 6.2