Physics 4410, Spring '99 Homework #4
Issued Wed, Feb 3 Due Wed, Feb 10
Required reading for this week: finish all of Griffiths 6.2.
1-i) Griffiths 6.3.
1-ii) Consider two identical spinless fermions in the same square well with the same delta function interaction as in Griffiths 6.3. Ignoring the interaction, find the ground state wave function, and its energy. Then, find the first order energy shift to the ground state induced by the interaction. (Explain briefly any interesting features of this last answer.)
2-i) Griffiths 6.4a. Just get a general formula, don't bother summing the series.
2-ii) Same as Griffiths 6.4a, but now look only at the ground state (n=1), and find the leading (first order) correction to the ground state wave function. (rather than the energy) Your answer will look like a sum of functions. Let Mathematica (or some other graphing calculator) sketch this sum for you. Does it make sense to you qualitatively? Briefly, discuss the graphical result.
3) Griffiths 6.4b
4) In this problem, you will work out the "finite nuclear size correction" in hydrogen. The potential felt by an electron due to a real proton (which has a finite size, R) is given by:
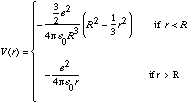
(I sketched this potential when we 1st started looking at perturbation theory. It's exactly the usual hydrogen potential for r>R, but doesn't go to -infinity at the origin, it flattens out when r < R ="size of the proton". You don't have to derive the above potential, it's a pretty straightforward application of Gauss' law. You can just use it...)
Calculate (using perturbation theory) the shift in energy for the hydrogen atom ground state (n=1, l=0, m=0) caused by the modification of the usual Coulomb potential to the one given above.
Do it all symbolically, but in the end, when you have a final formula, plug in values to also get the energy shift of the ground state, in eV. (Use R=1fm, a=0.5 Angstroms)
(Remember that the hydrogen unperturbed ground state energy is -13.6 eV. Do you think this effect is measurable?)