1) Use UNIT analysis to find quick and dirty approximate sol'ns to the following 3 parts:

i) A 3-dimensional harmonic oscillator has the potential . What is the shift in its ground state energy due to a small "anharmonic" perturbation of the form ?

ii) A particle is in a 1-dimensional infinite square well (size a). What is the shift in its ground state energy due to a perturbation which is + in the left half of the well, and - in the right half? (Note: Can you see why the first order correction to the ground state must be exactly zero? So, you'll have to estimate the second order correction here...)

iii) We solved Griffiths Problem 6.1 using perturbation theory on hw #3 (Problem "6-i"). Now, just estimate the answer using unit analysis.

In all 3 cases above, show and explain your work! (Can you argue the correct signs, too?)

2-i) Find the (normalized) eigenvectors and eigenvalues of the matrix

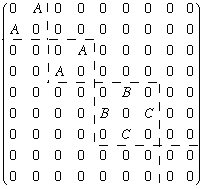
ii) Now do Griffiths problem 6.32. You do NOT need to work out any of the nonzero matrix elements, just use the results from Griffiths' "Partial answer".

Note: it appears that Griffiths left out one possible non-zero matrix element, namely

. However, it is zero - please show that it vanishes (from the angular integral).

When you are done, draw an energy level diagram for the n=3 Stark levels.

(Label the energy shifts carefully, and indicate what all the states are. Make your diagram large and readable!)

3) Griffiths 6.13

Hint: I claim for a harmonic oscillator: .
1 pt of extra credit for deriving this (hand it in to me separately)

4) Griff 6.14