 ,
for C and Lead on one graph, and compare with F+H Fig. 6.7. (It should agree
pretty well)
,
for C and Lead on one graph, and compare with F+H Fig. 6.7. (It should agree
pretty well)Issued Wed Feb 12 Due Wed, Feb 26
Required reading: F+H Ch. 6+7
1 i) Use F+H Eqn. 6.35 to find "c" and "a" for Carbon and Lead.
ii) Find numerical values for "N" in eq'n 6.32, for Carbon and Lead.
iii) Plot the charge distribution,
 ,
for C and Lead on one graph, and compare with F+H Fig. 6.7. (It should agree
pretty well)
,
for C and Lead on one graph, and compare with F+H Fig. 6.7. (It should agree
pretty well)
iv) Find
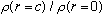 for C and Pb.
for C and Pb.
(Comment on the deviation from .5)
v) Find <r^2> numerically for C and Pb.
(Comment on the deviation from the "guestimate" 3c^2/5, and also from F+H Eq. 6.34. )
2) F+H 6.21
Hint: The magnetic moment of an ideal, pointlike p-pi system has several pieces which just add. There are the intrinsic (or "spin") magnetic moments arising from each object, given by F+H 5.15 (remember, g of an ideal proton is 2) and also there is the "orbital" magnetic moment, given correctly by F+H 5.14.
3) F+H 6.26. (Give your answer for t in (GeV/c)^2)
For the last part ("collisions with a heavy target), assume that you're looking for electrons scattering off of the *electrons* in the target (which you can assume are effectively at rest)
Hint1: t is the squared 4-momentum transfer, see Eq. 6-61.
Hint2: At what scattering angle do you get the largest momentum transfer, and hence the best look at structure?
4) F+H 7.5
(Hint: Earth is mostly iron, density = 6 g/cc. The solar constant, the average amount of solar energy hitting the earth, is about 1300 W/m^2)
5) F+H 7.7
(Hint: Assume liquid scintillators are water-like in all their properties)
In part a, give your answer in cm, and also in light years (!)
In part c, list any reactions you can think of that are allowed by conservation laws.
6) Consider elastic electron scattering off of a nucleus, mass M. (Assume the electron energy is high, so you can neglect the mass of the electron)
(over ->)
Prove the following:
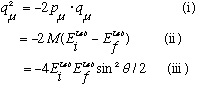
Here, q is the 4-momentum transferred,and p is the initial 4-momentum of the nucleus. Ei and Ef are the incident and final energies of the electrons. The angle theta is the scattering angle between incident and final electrons, in the lab frame. (The lab frame is the one where the incident nucleus is at rest)
4-vectors are defined as
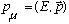 ,
where
,
where
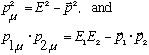
are frame independent "invariants". (See footnote on p. 139)
In the "Lab" frame,
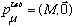 ,
but the outgoing nucleus is moving.
,
but the outgoing nucleus is moving.
You could of course shift to a different frame... For the next part, move to
the reference frame called the "Breit" or "Brick wall" frame, in which the
incoming nucleus is moving left with momentum
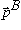 ,
and the outgoing nucleus is moving right with exactly equal and opposite
momentum,
,
and the outgoing nucleus is moving right with exactly equal and opposite
momentum,
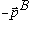 .
.
iv) Find the magnitude of
 in terms of the invariant quantity
in terms of the invariant quantity
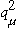
| 4420 main page | Prof. Pollock's page. | Physics Dep't | Send mail |