Wave mechanics in three dimensions
Now we're ready to return to wave mechanics and tackle some three-dimensional problems. As always, it's useful to start with the free-particle solution and see what it looks like; that will also give us a handle on problems with regions of constant potential.
First, a quick aside: we're starting to work with a lot of special functions right now. Sometimes you may be able to use Mathematica to work with them, but it's often useful to really know certain identities, limiting forms, and so forth, to simplify before you plug in to the computer. In our own backyard, NIST maintains the "Digital Library of Mathematical Functions", http://dlmf.nist.gov. Wolfram also maintains a detailed repository of information on functions at http://functions.wolfram.com.
Let's go all the way back to where we separated the Schrödinger equation into radial and angular parts. The equation for the radial part was:
\[ \begin{aligned} \left[ -\frac{\hbar^2}{2mr^2} \frac{d}{dr} \left( r^2 \frac{d}{dr} \right) + \frac{l(l+1)\hbar^2}{2mr^2} + (V(r) - E) \right] R_{El}(r) = 0. \end{aligned} \]
If we make the substitutions
\[ \begin{aligned} k = \frac{\sqrt{2m(E-V(r))}}{\hbar}, \\ \rho = kr, \end{aligned} \]
then this simplifies to a standard form:
\[ \begin{aligned} \frac{d^2 R}{d\rho^2} + \frac{2}{\rho} \frac{dR}{d\rho} + \left[ 1 - \frac{l(l+1)}{\rho^2} \right] R = 0. \end{aligned} \]
You may recognize this differential equation: its solutions are the spherical Bessel functions,
\[ \begin{aligned} j_l(\rho) = (-\rho)^l \left[ \frac{1}{\rho} \frac{d}{d\rho} \right]^l \frac{\sin \rho}{\rho}, \\ n_l(\rho) = - (-\rho)^l \left[ \frac{1}{\rho} \frac{d}{d\rho} \right]^l \frac{\cos \rho}{\rho}. \end{aligned} \]
The latter functions are sometimes called the spherical Neumann functions, or just "spherical Bessel functions of the second kind." The \( j_l \) are well-behaved as \( \rho \rightarrow 0 \), but the \( n_l \) are singular, so for any application including the origin we can discard the \( n_l \). This is easy to see from the asymptotic behavior: as \( \rho \rightarrow 0 \), we find
\[ \begin{aligned} (\rho \rightarrow 0): \begin{cases} j_l(\rho) \approx \frac{\rho^l}{(2l+1)!!} \\ n_l(\rho) \approx -\frac{(2l+1)!!}{\rho^{l+1}}. \end{cases} \end{aligned} \]
In the other asymptotic limit, we find
\[ \begin{aligned} (\rho \rightarrow \infty): \begin{cases} j_l(\rho) \approx \frac{1}{\rho} \sin \left(\rho - \frac{l\pi}{2} \right) \\ n_l(\rho) \approx -\frac{1}{\rho} \cos \left(\rho - \frac{l\pi}{2} \right). \end{cases} \end{aligned} \]
Both functions are clearly vanishing as \( \rho \rightarrow \infty \), so they will give properly normalized wavefunctions in that limit. The spherical Bessel functions can be written in terms of the ordinary Bessel functions:
\[ \begin{aligned} j_n(x) = \sqrt{\frac{\pi}{2x}} J_{n+1/2}(x) \\ n_n(x) = \sqrt{\frac{\pi}{2x}} Y_{n+1/2}(x) = (-1)^{n+1} \sqrt{\frac{\pi}{2x}} J_{-n-1/2} (x). \end{aligned} \]
Here's what the first couple of spherical Bessel functions look like:
\[ \begin{aligned} j_0(\rho) = \frac{\sin \rho}{\rho} \\ n_0(\rho) = -\frac{\cos \rho}{\rho} \\ j_1(\rho) = \frac{\sin \rho}{\rho^2} - \frac{\cos \rho}{\rho} \\ n_1(\rho) = -\frac{\cos \rho}{\rho^2} - \frac{\sin \rho}{\rho} \end{aligned} \]
With this setup, it's quite straightforward to find the solution to the infinite spherical well,
\[ \begin{aligned} V(r) = \begin{cases} 0, & r \leq R \\ \infty, & r > R. \end{cases} \end{aligned} \]
With the origin included in our physical region of interest, the spherical Neumann functions must vanish, and then the spherical Bessel functions have to vanish at the infinite wall, i.e.
\[ \begin{aligned} j_l(kR) = 0. \end{aligned} \]
For \( l=0 \) these are just the zeroes of \( \sin \rho / \rho \), i.e. \( kR = \pi, 2\pi, 3\pi, ... \), which gives us the quantized energies
\[ \begin{aligned} E_{l=0} = \frac{\hbar^2}{2mR^2} \left[ \pi^2, 4\pi^2, 9\pi^2, ... \right] \end{aligned} \]
For higher \( l \) we can only solve for the zeroes of the spherical Bessel functions numerically. Thus, we have an infinite series of bound-state energies \( E_{nl} \) for each \( l \), and the total wavefunction can be written
\[ \begin{aligned} \psi_{nlm}(\rho, \theta, \phi) = A_l\ j_l(k_nr) Y_l^m (\theta, \phi). \end{aligned} \]
We can, in principle, determine the constants \( A_l \) by integrating the absolute value squared of the wavefunction. Of course, the properties of the spherical harmonics guarantee that the angular part of the integral is already normalized, so we just have to insist that
\[ \begin{aligned} \int_0^R dr\ r^2 |A_l|^2 j_l^2(k_n r) = 1. \end{aligned} \]
Once again we'll only really find nice analytic results for \( l=0 \), and we'll have to resort to numerics beyond that point.
What happens if the well is finite? Let's look at the case
\[ \begin{aligned} V(r) = \begin{cases} 0, & r \leq R \\ V_0, & r > R \end{cases} \end{aligned} \]
Outside the well region, for \( r>R \), we can include both the \( j_l \) and \( n_l \) in our solution. However, let's consider what happens if we have a bound state, \( 0 < E < V_0 \). As usual, to maintain the same differential equation and keep our variables real, we let \( k=i \kappa \), i.e.
\[ \begin{aligned} \kappa = \sqrt{2m(V(r)-E)} / \hbar. \end{aligned} \]
Our solutions are still spherical Bessel functions in exactly the same way, but now with \( k \rightarrow i \kappa \), and thus \( \rho = i \kappa r \). Now, we know that our solutions have to vanish as \( r \rightarrow \infty \); what do the imaginary versions of \( j_l \) and \( n_l \) behave like? Rewriting the asymptotic formulas from above and now letting \( \rho = \kappa r \), we find
\[ \begin{aligned} j_l(i\kappa r) \rightarrow \frac{-i}{\kappa r} \sin \left( i\kappa r - \frac{l\pi}{2} \right) \\ = \frac{1}{\kappa r} [\cos (l\pi/2) \sinh (\kappa r) + i \sin (l\pi/2) \cosh (\kappa r)], \\ n_l(i\kappa r) \rightarrow \frac{i}{\kappa r} \cos \left( i\kappa r - \frac{l\pi}{2} \right) \\ = \frac{1}{\kappa r} [ - \sin (l\pi/2) \sinh (\kappa r) + i \cos (l\pi / 2) \cosh (\kappa r)]. \end{aligned} \]
Unfortunately for us, \( \sinh \) and \( \cosh \) both diverge as \( r \rightarrow \infty \), so we can't write the solution as an arbitrary sum of \( j_l \) and \( n_l \) components; we have to take a particular combination. From the asymptotic forms above, it's easy to see what the right basis to use is:
\[ \begin{aligned} h_l^{(1)}(\rho) = j_l(\rho) + i n_l(\rho) \\ h_l^{(2)}(\rho) = j_l(\rho) - i n_l(\rho). \end{aligned} \]
These are known as spherical Hankel functions of the first and second kind. Their asymptotic behavior is easy to work out from the asymptotic formulas above: we have
\[ \begin{aligned} h_l^{(1)}(\rho) \rightarrow \frac{-1}{\kappa r} [\cos (l\pi/2) - i \sin (l\pi/2)] [\cosh(\kappa r) - \sinh(\kappa r)] \\ = \frac{-i^{-l}}{\kappa r} e^{-\kappa r} \\ h_l^{(2)}(\rho) \rightarrow \frac{1}{\kappa r} [\cos (l\pi/2) + i \sin (l\pi/2)] [\cosh (\kappa r) + \sinh(\kappa r)] \\ = \frac{i^{l}}{\kappa r} e^{\kappa r}. \end{aligned} \]
So the Hankel functions have the correct asymptotic behavior; for a bound state, only the solution of the first type \( h_l^{(1)}(\rho) \) is allowed.
If we think of the spherical Bessel functions as analogous to sines and cosines, then the spherical Hankel functions are the equivalent of complex exponentials. Just like one-dimensional wave mechanics problems, one description may be more useful than the other, depending on what problem we're trying to solve. In particular, like the plane-wave solutions the Hankel functions correspond to spherical waves which are incoming (first type) and outgoing (second type) with respect to the origin. This is a particularly useful way to formulate things if we're interested in scattering of waves off of a target.
Spherically symmetric potentials, in general
Now that we've done one useful example, let's step back and obtain some general understanding about spherically symmetric potentials, starting with the replacement
\[ \begin{aligned} R_{El}(r) = \frac{u_{El}(r)}{r}. \end{aligned} \]
This changes the radial equation into a more familiar form:
\[ \begin{aligned} -\frac{\hbar^2}{2m} \frac{d^2 u_{El}}{dr^2} + \left[ \frac{l(l+1)\hbar^2}{2mr^2} + V(r) \right] u_{El}(r) = E u_{El}(r). \end{aligned} \]
This is exactly the one-dimensional Schrödinger equation in \( r \), with an extra "centrifugal" contribution to the potential energy; we write the combination as an effective potential,
\[ \begin{aligned} V_{\textrm{eff}}(r) = V(r) + \frac{l(l+1) \hbar^2}{2mr^2}. \end{aligned} \]
The second term is sometimes called a "centrifugal barrier", since for \( l \neq 0 \) it acts to repel the particle from the origin. Everything is self-consistent with treating the radial part of the solution as a separate one-dimensional system; for example, since the spherical harmonics are already normalized, the normalization condition for the wavefunction is just
\[ \begin{aligned} \int dr\ r^2 |R_{El}(r)|^2 = \int dr |u_{El}(r)|^2 = 1. \end{aligned} \]
If the potential energy \( V(r) \) doesn't diverge more strongly than \( r^2 \) as \( r \rightarrow 0 \), i.e. if
\[ \begin{aligned} \lim_{r \rightarrow 0} r^2 V(r) = 0, \end{aligned} \]
then near the origin the centrifugal term must be dominant, leading to the simplified equation (in the limit \( r \rightarrow 0 \))
\[ \begin{aligned} \frac{d^2 u_{El}}{dr^2} = \frac{l(l+1)}{r^2} u_{El}(r) \end{aligned} \]
which is solved by
\[ \begin{aligned} u_{El}(r) = A r^{l+1} + Br^{-l}. \end{aligned} \]
Notice that these match the asymptotic behaviors of the spherical Bessel functions for small \( r \), as they must since \( V(r) = 0 \) is certainly not divergent anywhere. The \( B \) solution has to be discarded if we include the origin in our region of interest, since it gives a singular wavefunction. In fact, even if we just consider solutions for a small region around the origin, as long as \( V(r) \) is negligible we have to set \( B=0 \) to avoid violating conservation of probability, as a calculation of the probability flux shows. (The details are in Sakurai.) As a consequence, we find that as \( r \rightarrow 0 \), the radial wavefunction universally takes the form
\[ \begin{aligned} R_{El}(r) \rightarrow r^l. \end{aligned} \]
For an electron in an atom, for example, the probability of finding it in the vicinity of the nucleus goes as \( (R_N / a_0)^{2l} \), where \( R_N \) is the nuclear radius and \( a_0 \) is the Bohr radius. This simple observation lets us immediately make some powerful observations about atomic structure; this is jumping ahead a bit, but I'll draw on ideas you should have seen before. We know that the spectrum of hydrogen atoms is reasonably well-described by the Bohr formula,
\[ \begin{aligned} E_n = \frac{-13.6\ \mbox{eV}}{n^2}, \end{aligned} \]
where \( n \) corresponds to the orbital energy level. We might expect that the Bohr model would also work well for a certain class of other atoms, namely the alkali metals, which have a complete set of full orbitals up to some \( N \), and then a single electron in orbital \( N+1 \). In fact, the Bohr formula sort of works: here is what is observed experimentally for lithium (\( N=2 \)) and sodium (\( N=3 \)):
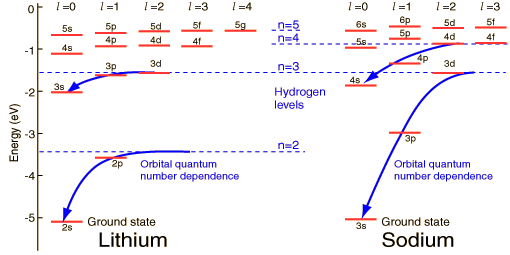
(the above picture is from the HyperPhysics website.)
The most significant deviations from the Bohr formula occur for the smallest \( l \) states in each orbital; these are precisely the states with wavefunctions that overlap significantly with the origin. These electrons can "see inside" the lower filled orbitals, and as a result are sensitive to the additional structure and stronger nuclear charge of the heavier elements.
Finally, we can also study the opposite limit \( r \rightarrow \infty \). Once again assuming the potential is well-behaved, this time that \( V(r) \rightarrow 0 \) as \( r \rightarrow \infty \), then the centrifugal contribution vanishes. If we have a bound state \( E<0 \), then the equation becomes
\[ \begin{aligned} \frac{d^2 u_E}{dr^2} = \frac{-2mE}{\hbar^2} u_E. \end{aligned} \]
We find decaying exponential behavior, \( u_E(r) \propto e^{-\kappa r} \), where as usual \( \kappa = \sqrt{-2mE} / \hbar \). Thus, for a bound state in any potential which vanishes at infinity and isn't "too singular" at the origin, we know immediately what the asymptotic form looks like.
In fact, it's often useful to "scale out" these asymptotic behaviors, and solve for the modified function
\[ \begin{aligned} w_{El}(\rho) = \rho^{-(l+1)} e^{\rho} u_{El}(\rho), \end{aligned} \]
leading to the modified differential equation
\[ \begin{aligned} \frac{d^2 w}{d\rho^2} + 2 \left( \frac{l+1}{\rho} - 1 \right) + \left[ \frac{V}{E} - \frac{2(l+1)}{\rho} \right] w = 0. \end{aligned} \]
This is the best setup to deal with the Coulomb potential.
The isotropic harmonic oscillator
Now we'll consider a less trivial problem; a version of the harmonic oscillator which is spherically symmetric, i.e.
\[ \begin{aligned} \hat{H} = \frac{\hat{\vec{p}}^2}{2m} + \frac{1}{2} m \omega^2 r^2. \end{aligned} \]
Once again, now that we're dealing with more complicated differential equations it's handy to rescale all our variables to be dimensionless. We make the replacements
\[ \begin{aligned} E = \frac{1}{2} \hbar \omega \lambda, \\ r = \sqrt{\frac{\hbar}{m \omega}} \rho, \end{aligned} \]
which gives for the radial equation
\[ \begin{aligned} \frac{d^2 u}{d\rho^2} - \frac{l(l+1)}{\rho^2} u(\rho) + (\lambda - \rho^2) u(\rho) = 0. \end{aligned} \]
Note that we can't rewrite this in terms of the asymptotically rescaled function \( w(\rho) \), because one of the conditions is violated: the potential energy no longer vanishes as \( r \rightarrow \infty \). We can still rescale to remove the short-distance asymptotic behavior, and anticipating the result I'll include an exponential rescaling factor too:
\[ \begin{aligned} u(\rho) = \rho^{l+1} e^{-\rho^2 / 2} f(\rho). \end{aligned} \]
(I'm following Sakurai in the inclusion of the mysterious-looking exponential factor here. We could just as easily have only scaled out the \( \rho \rightarrow 0 \) behavior; the resulting differential equation is a little more difficult to deal with using the technique we're about to introduce.)
Next time: we finish the solution.