Course Info » Exam Info
Exam Information
There will be three midterms and a final:
| Exam | Date | Time | Location |
|---|---|---|---|
| Midterm 1 (See below for more info) |
Thurs, Feb 6 |
7:30-9:15 PM |
If your TA is Rosemary Wulf, or Andrew Hess, go to G1B30 (our regular class) If your TA is Jake Fish or Clarissa Briner, go to G1B20 (next door, the OTHER big lecture hall) |
| Midterm 2 (See below for more info) |
Thurs, Mar 6 |
7:30-9:15 PM |
SAME AS LAST TIME! |
| Midterm 3 (See below for more info) |
Thurs, Apr 10 |
7:30-9:15 PM |
SAME AS THE LAST TIME! |
| Final (See below for more info) |
Mon May 5 |
1:30-4 PM |
NEW: We only have our classroom (G1B30) for the final. Those of you who were assigned to the other room will need to come to the regular classroom for the final! |
Exams will be cumulative, and will be a multiple choice. Calculators with scientific notation are allowed. (Of course, no phones, internet access, "electronic crib sheets", etc!) Graphing calculators are ok too, just don't use them to store stuff - that's what your crib sheet is for. You may bring a single side of 8.5 in. x 11 in. paper to the first exam, with your own handwritten notes. You will be allowed to add one more side of notes for each midterm. (So, the 2nd midterm you may use BOTH sides of that crib sheet, for the 3rd midterm you can add the front of a second page, and for the final, both sides of both crib sheets)
Click here to skip all the way down to old Exam 1 info
Click here to skip all the way down to old Exam 2 info
Click here to skip all the way down to old Exam 3 info
__________________________________________________________________________________________________
OUTCOME INFORMATION For Final Exam:
Here is the histogram of scores (after dropping 1 question out of 39)
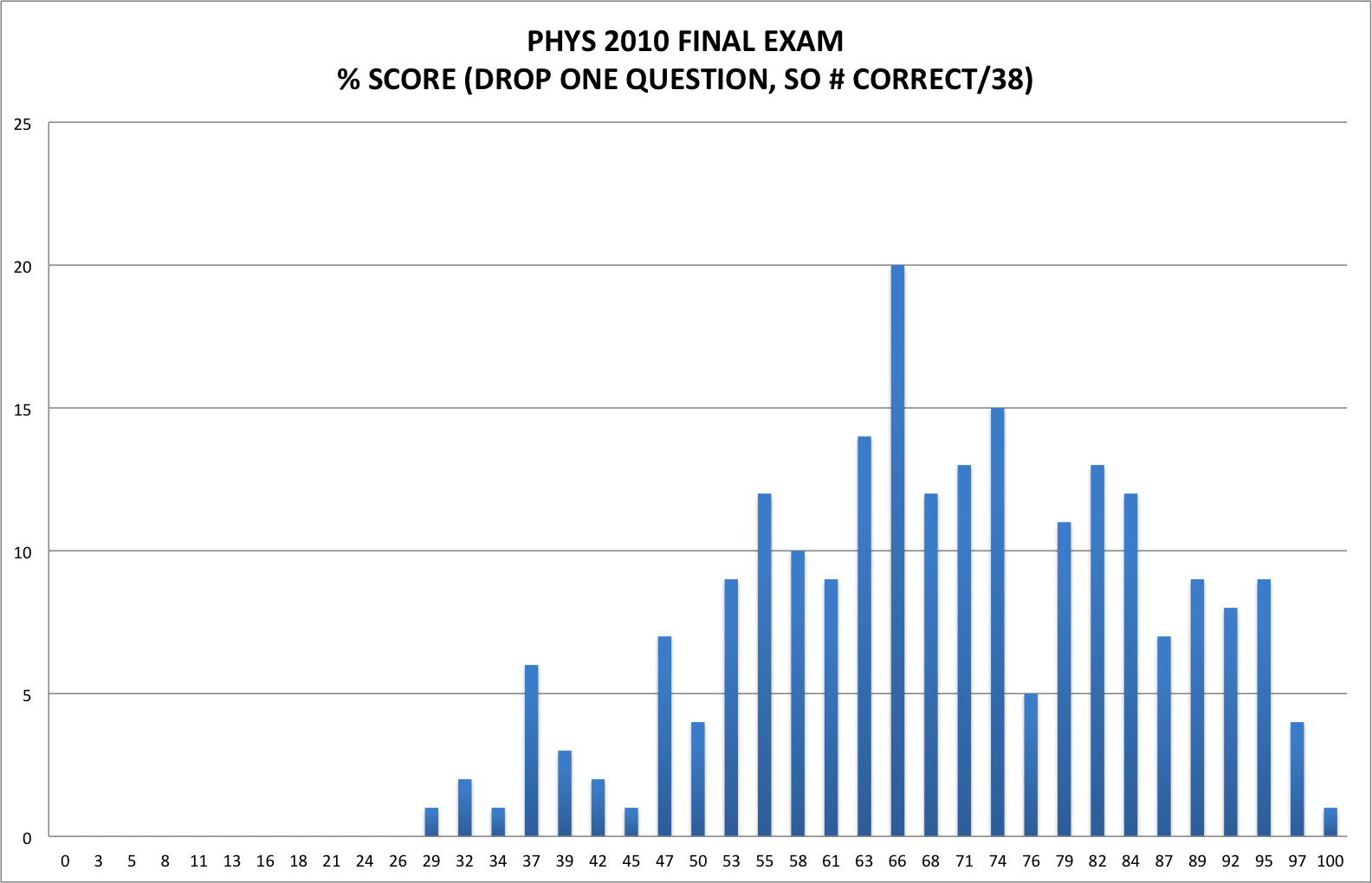
(Note: To convert this exam to a percent, we divided your score by 38, not 39. That is the same as dropping one missed question. Except if you got a perfect score, (congrats!) - then we didn't drop anything, and just computed your score in the usual way, 100%)
- The average score (computed this way) was 69% (pretty much the same as the midterm average)
- The median was 68% (That means half the class scored above 68%).
- The "Standard Deviation" was 17%.
Total course scores are now available on D2L. For information on how exactly your course letter grade is computed, please see our detailed grade info page.
OLDER: STUDY INFORMATION FOR Final exam:
The final will be cumulative, covering everything we have done all term. There will, however, be an emphasis on newer material since the 3rd midterm (which includes the parts of Ch 8, 9, and 10 we have covered - see below). I would expect roughly half (maybe a bit less) of the final to be older/review material, and half (or more) to be newer stuff. (Think of it as "exam 4" plus "some review") The final runs for 2.5 hours, and will probably have something like ~40 multiple choice questions, give or take.
For studying, as always, check out the Giancoli 5th Edition Website, he has nice sample problems and there are practice tests there too (with answers!) Look e.g. for the "practice questions" and also the "MCAT practice problems".
- There is also, as usual, a practice exam from a previous semester on our D2L page.
- There will also, like last time, be a shorter practice exam in recitation the last week.
For the new material on the final exam, here are some examples of our learning goals for new material (see below in this page for earlier goals). Each bullet below should be preceeded by You are expected to....
Chapter 8 Rotational motion. NOTE: We skipped Ch 8.9 (vector nature of angular variables)
... be able to convert degrees to radians and vice versa
... be able to work with angles in radians, including working your calculator, and know the definition of the radian
... define angular velocity including dealing with mixed units (like rpm, revolutions per minute, and radians/sec) and relate frequency and period as well.
... connect angular velocity (omega, in rad/sec) to speed and radius for circular motion (omega = v/r)
... use the above to compute centripetal acceleration for uniform circular motion (a = v^2/R) when one knows angular velocity instead of linear velocity (a = omega^2 R)
... relate "tangential" acceleration to angular acceleration, and graphically visualize both components of acceleration in rotating scenarios
... solve "constant angular acceleration" kinematics problems (much as we did constant acceleration problems back in Ch 2)
... relate the linear motion of a bicyle (velocity and acceleration) to the angular variables on the wheels
... Compute the torque of a force about an arbitrary axis (including getting the "perpendicular component" correct, and getting the sign correct using our convention that Clockwise is negative)
... compute the moment of inertia of a simple system of point masses
... use Newton's law in angular form (Torque = I * alpha) to solve basic rotating dynamics problems. (Basically, recognizing when this formula can be used, computing the total torque with proper signs, being able to properly use a table to find the appropriate moment of inertia for sphere, disk, hoop, or rod)
... compute the rotational energy of rolling or spinning objects, and use this as part of "conservation of energy" questions. This includes recognizing WHEN conservation of mechanical energy is helpful (e.g, no frictional losses of energy)
... compute the angular momentum of rolling or spinning objects, and use this as part of "conservation of angular momentum" problems. This includes recognizing WHEN conservation of angular momentum is helpful (namely, when net external torque on your system is zero)
We skipped 8.9
Chapter 9 Static Equilibrium. (NOTE: We skipped Ch.9.4 through 9.7, we only did the first part of this chapter)
...recognize situations of static equilibrium, and be able to write out the conditions (F_net=0, Torque_net=0)
... be able to draw and use "extended free body diagrams"
... to use extended free body diagrams with the above equilibrium equations to solve for unknowns.
We skipped 9.4 on, so we won't ask questions about stability, or stress/strain...
Chapter 10 Fluids. (Note: We skip Ch 10.8 through 10.14, we only did the first half of this chapter)
... identify the main differences between solid, liquid, and gas as outlined by Giancoli in 10.1
... know the definition of density, and be able to use it in basic questions relating mass to volume
... know the definition of pressure, and use it to relate force, area, and pressure. (This includes knowing units, and directions. Pressure is a scalar, but force is a vector, you should be able to identify the direction of the force on a surface caused by pressure)
... know and use the formula which relates pressure to depth in an (incompressible) fluid
... answer qualitative and quantitative questions about gauge and absolute pressure (like how high water rises in a straw for a given difference in pressure top to bottom)
... use Pascal's principle to relate pressure in odd-shaped containers at different points, and also to relate force/area in hydraulics.
... state Archimede's principle, and be able to use it to compute buoyancy, and solve questions regarding sinking and floating, and "apparent weight" under water.
... be able to identify "displaced volume" of objects submerged, or partially submerged, in a fluid.
We skipped 10.8 on
Chapter 11 Simple Harmonic Motion (Note: Very little of this chapter will be covered, just 11.1 and 11.2. We will finish the term talking about it, but the exam will only cover the aspects of the first bits of this chapter that relate back to our earlier coverage of springs. So, you will need to review the physics of Hooke's law (F = -kx for a spring) and energy of a spring (1/2 k x^2)
It turns out that most of
11.1 and 11.2 is largely review!
___________________________________________________________________________________________
Outcome INFORMATION FOR EXAM 3:
The class did fine on exam 3, better than exam 2! Here is the histogram of scores (after dropping 1 question out of 24)
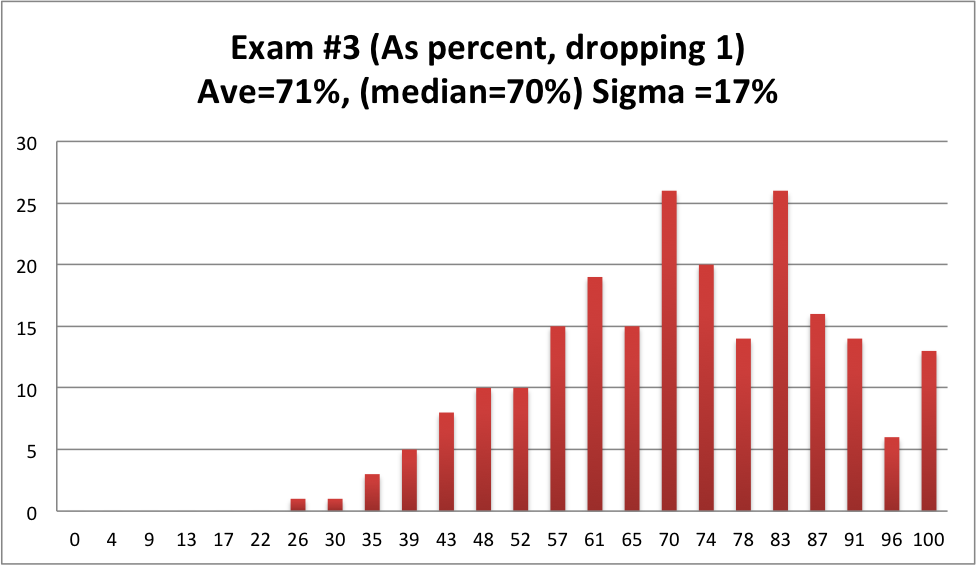
(Note: To convert this exam to a percent, we divided your score by 23, not 24. That is the same as dropping one missed question. Except if you got a perfect score, (congrats!) - then we didn't drop anything, and just computed your score in the usual way, 100%)
- The average score (computed this way) was 71% (5 points higher than the last midterm)
- The median was 70% (That means half the class scored above 70%).
- The "Standard Deviation" was 17%.
- We don't assign letter grades to exams. Neither should you . Only your total combined course score matters for your final grade! (See immediately below)
If you are really unhappy about your score, please read this page. It has suggestions for concrete steps you might take. Also note the "resources" link at the top right of our course pages. After reading these, if you'd like to come see Prof. Pollock or Prof Uzdensky, check out the "Help Room hours" link, or the "contacts" link, or just email us, or visit before/after class.
If you have serious concerns about the exam scoring, contact Steven.Pollock (at) Colorado.edu. Note that I keep all bubble sheets (which ALWAYS take precedence over what you circled on the exam)
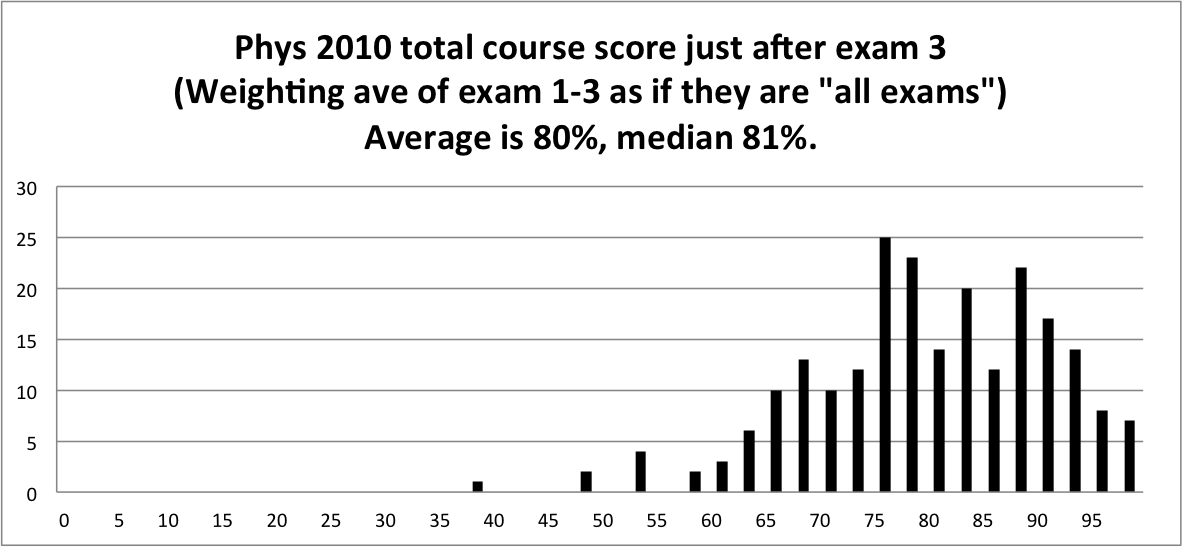
Again, we don't assign letter grades to individual exams. Only your total course score determines your grade. See the syllabus for the weights of various course components. Here is a distribution of "total course score" so far (To compute this, I assumed your future exam scores will match the average of exams 1-3, that your future homeworks will match the ones so far, etc.) The class is doing fine, even without any curving, more than half the class is getting A's and B's. Keep it up!
Older STUDY INFORMATION FOR EXAM 3:
Check out the Giancoli 5th Edition Website, he has nice sample problems and there are practice tests there too (with answers!) Look e.g. for the "MCAT practice problems", those are often decent.
Expect to see questions you have never seen before (we do not repeat problems we've already asked you!) but they will be similar to what you work on in clicker questions, recitation/labs, text examples, and the homeworks. We want you to show off your conceptual and computational/problem-solving skills, we're interested in your understanding of the physics, we are not interested in memorization or plug-n-chug behaviour or rote procedures.
For the third exam, here are some examples of our learning goals for new material (see elsewhere for earlier goals).
Each bullet below should be preceeded by You are expected to....
Chapter 5 Circular Motion.
... know when the formula a = v^2/R (centripetal acceleration) is applicable (uniform circular motion, steady speed)
... solve basic Newton's 2nd law problems when an object is moving with uniform circulation motion, which includes setting up a free-body diagram, writing down, and solving Newton's second law
... solve basic Newton's 2nd law problems when an object is in free fall, (the "weightlessness" condition)
... use Newton's Universal Law of gravitation, which includes identifying problems where it is applicable, identifying the quantities involved in the formula (masses, and distance between them), and using it as part of a Newton's second law problem involving gravitating bodies.
... connect g (little g, 9.8 m/s^2) to G (big G, the constant in Newton's law of University gravity), and extend this connection to other planets where the value of "g" might be different than earth.
... be able to use Kepler's third law to relate period, orbital radius, and the mass of the "central body", both quantitatively and qualitatively.
... Use Newton's law of gravity (with Newton's 2nd law, and the basic definition of speed) to relate orbital speed (in a uniform circular orbit) to radius..
Chapter 6 Work and energy.
NOTE: We skipped 6.2
... know the basic definition of work done by a given force, and be able to compute it even when the force and displacement do not "line up". This includes getting the SIGN of work correct!
... know the basic definition of kinetic energy, and thus be able to compute KE, and changes in KE.
... distinguish between "net work" and "work done by a particular force"
... know and propery use metric units for work and energy (the definition of the Joule)
... use the work-energy principle to relate net work done and the change in kinetic energy of an object
... know the formulas for potential energy (PE) arising from gravity near the surface of the earth (mgy) and also from an object on an ideal spring (1/2 k x^2)
... know and use Hooke's law (F = -kx) in problems involving masses connected to springs, including interpreting the sign in Hooke's law correctly)
... use the principle of conservation of energy to solve basic problems in 1- and 2-d involving objects where energy changes form (from kinetic to various forms of potential energy) This includes recognizing problems where mechanical energy is or is not conserved (e.g. when frictional forces are present, or external forces)
... solve basic problems where friction or external forces are involved, still using the principle of conservation of energy, but now including the "W_friction + W_external" term to relate initial energy to final energy of a given system. (This will require knowing the sign of those extra work terms)
... know the basic definition of power (change in energy/change in time), and the alternative form (force_parallel times speed) to be able to compute or compare powers
Chapter 7 Momentum and momentum conservation
NOTE: We skipped 7.7 - 7.10!
... use the basic definition of momentum (mv) to compute momentum of objects and systems of objects. This includes recognizing the VECTOR nature of momentum, and thus being able to add vectors when you have a system, and find specific components (x, or y) of momentum.
...use the basic definition of impulse (Change in momemtum) to be able to compute impulse given initial and final momenta. (That includes 2-dimensional situations where you are subtracting vectors, and 1-d situations where you must consider the SIGNS of the momenta involved, not just their magnitudes)
... relate change in momentum to force and time intervals (F = Delta p / delta t)
... know the principle of conservation of momentum, which means recognizing situations where it applies (generally, systems where there is no EXTERNAL net force) and be able to use it to solve basic problems, typically involving collisions
... know the terminology "elastic, inelastic, and totally inelastic" collisions, and be able to relate "before and after" quantitaties in all 3 of those cases. We will stick to 1-dimensional problems for our collision problems on the exam.
... be able to recognize "ballistic pendulum" problems where a collision happens (involving conservation of momentum, for "immediately before to immediately after" the crash), followed up by something further (like a pendulum rising, or a spring compressing, or a combined system rising in the air) where the second portion involves a different principle, like conservation of energy.
Chapter 8 Rotational motion
NOTE: The third midterm exam will not explicitly cover Ch 8 material.
However, the following topics (from the very beginning of Ch 8) are largely not really new, and may still be helpful to study just to review the "circular motion" material from Ch 5 as well.
... be able to convert degrees to radians and vice versa
... be able to work with angles in radians, including working your calculator, and knowing the definition of the radian
... define angular velocity including dealing with mixed units (like rpm, revolutions per minute, and radians/sec) and relating frequency and period as well.
... connect angular velocity (omega, in rad/sec) to speed and radius for circular motion (omega = v/r)
... use the above to compute centripetal acceleration for uniform circular motion (a = v^2/R) when one knows angular velocity instead of linear velocity (a = omega^2 R)
(But e.g. we will NOT be asking you questions on the 3rd midterm requiring the "angular kinematics" equations or "tangential acceleration" or "angular acceleration". That's for the final....)
___________________________________________________________________________________________
The class did fine overall on exam 2, although it was harder than the first midterm.
Here is the histogram of scores after dropping one:
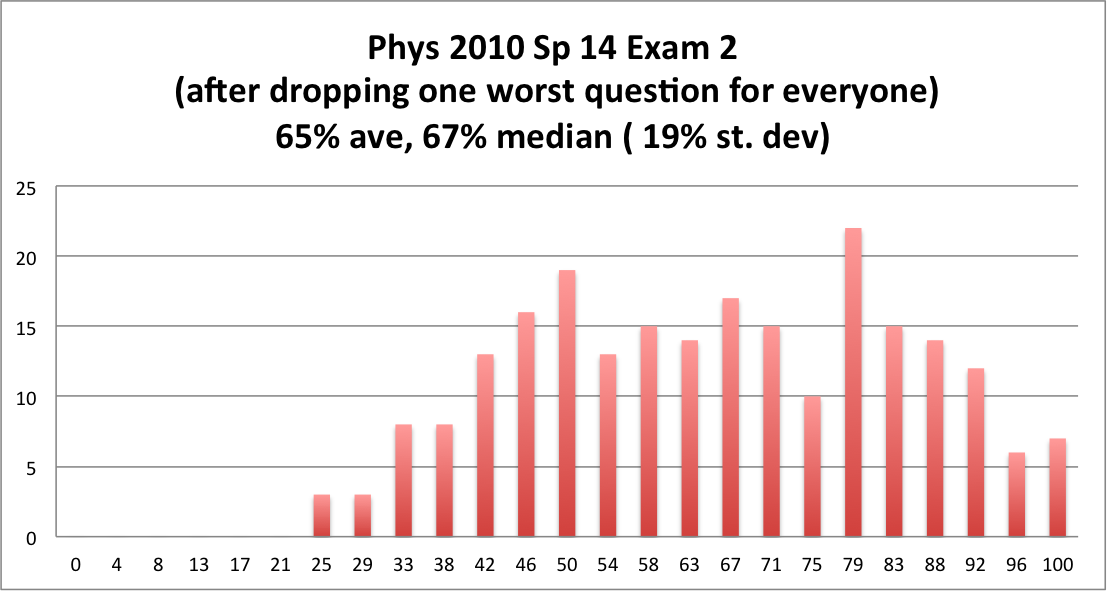
(Note: To convert this exam to a percent, we divided your score by 24, not 25. That is the same as dropping one missed question. Except if you got a perfect score on the Multiple Choice, (congrats!) - then we didn't drop anything, and just computed your score in the usual way, 100%)
- The average score (computed this way) was 65%
- The median was just below 67% (That means half the class scored above 67%).
- The "Standard Deviation" was 19%.
- We don't assign letter grades to exams. Neither should you . Only your total combined course score matters for your final grade! (See immediately below)
If you are really unhappy about your score, please read this page. It has suggestions for concrete steps you might take. Also note the "resources" link at the top right of our course pages. After reading these, if you'd like to come see Prof. Pollock or Prof Uzdensky, check out the "Help Room hours" link, or the "contacts" link, or just email us, or visit before/after class.
If you have serious concerns about the exam scoring, contact Steven.Pollock (at) Colorado.edu. Note that I keep all bubble sheets (which ALWAYS take precedence over what you circled on the exam)
Again, we don't assign letter grades to individual exams. Only your total course score determines your grade. See the syllabus for the weights of various course components. Here is a distribution of "total course score" so far (To compute this, I assumed your future exam scores will match the average of exams 1&2, that your future homeworks will match the first few, etc.) The class is doing fine, even without any curving, more than half the class is getting A's and B's. Keep it up!
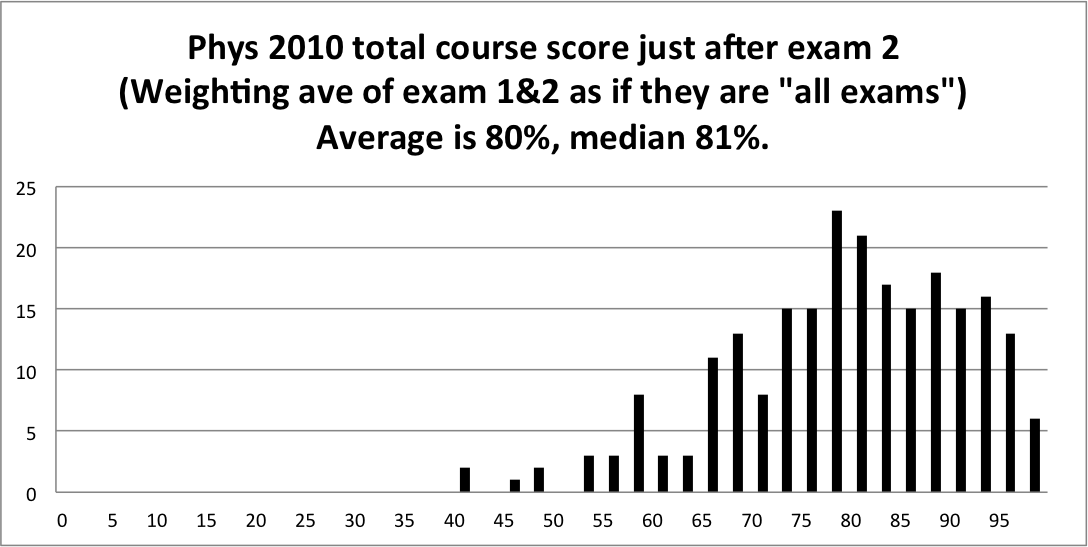
OLDER: STUDY INFORMATION FOR EXAM 2:
Here are the FRONT TWO PAGES of the 2nd exam (including my crib sheet! No need for you to duplicate anything I have on yours if you don't want!)
Like exam 1: 2 PRACTICE EXAMS are posted on our D2L page. On the "Course Home" page, look for the "content browser" window and go to "exams". You certainly do NOT have to do these, they are just there if you want some extra practice. (They are from two different instructors, with somewhat different styles from ours. The timing of exams is never the same, so there may be a couple of questions on topics we haven't quite covered yet. See below, I'll update our expected coverage as we get closer to the exam)
There will again be an evening review session 5-6:30 PM in G125 on Tues Mar 4. It will be very informal, just a time/space to ask questions. (Most likely we will go over the practice test questions, that's what usually ends up happening!)
TA Rosemary Wulf will likely run this.
The second midterm covers material from the course through the end of the week before the exam (Feb 28):
It is cumulative, (this is the nature of physics) but with a strong focus on new material since the first midterm. (So, see above, under exam 1, for more useful information about older material to review/study)
This includes anything covered in lecture, posted lecture notes, recitation/lab activities weeks 1-8, CAPA 1-7, Written Homeworks 1-5, or Giancoli Ch. 1-5.7, all fair game!
Other review options: read the text! Look for the Conceptual Examples scattered througout. Your goal in studying should be to keep trying FRESH problems, it doesn't do much good to try to memorize/repeat old ones. Look at the "Questions" at the end of each chapter (These come before the "Problems", which tend to be more computational. The exam will be a mix, but I would say slightly more "concept question-like" than "computational" on the whole)
Check out the Giancoli 5th Edition Website, he has nice sample problems and there are practice tests there too (with answers!) Look e.g. for the "MCAT practice problems", those are often decent.
Expect to see questions you have never seen before (we do not repeat problems we've already asked you!) but they will be similar to what you work on in clicker questions, recitation/labs, text examples, and the homeworks. We want you to show off your conceptual and computational/problem-solving skills, we're interested in your understanding of the physics, we are not interested in memorization or plug-n-chug behaviour or rote procedures.
For the second exam, here are some examples of our learning goals for new material (see above for earlier goals).
Each bullet below should be preceeded by You are expected to....
Chapter 3 (continued) Projectile Motion.
... recognize problems which are 2-dimensional "free fall" (without being explicitly told) and be able to set up and solve the usual equations of motion in x and y-directions (which includes times, distances in x, and y, and velocities)
... use "unstated" elements of free fall problems (e.g. acceleration is -g in the y-direction if we call up "positive", but acceleration is 0 in the x-direction, the y-component of velocity is zero at the peak, etc)
... draw and/or interpret diagrams involving projectile motion, and be able to extract or solve for the x- and y-components of all vectors involved.
... Find differences of vectors either graphically or through components, and thus e.g. relate initial and final position vectors to Delta x, and final relating that to average velocity, all in 2-D (and similarly for velocities/average acceleration)
... distinguish between speed and velocity (which is a vector) in 2-D problems
Note that we did not explicitly cover sections. 3.7 or 3.8
Chapter 4 Newton's Laws.
... draw a proper free-body diagram, labeling forces: force ON object BY another object, and identifying what kind of force (tension, gravity, normal, friction)
... apply Newton's second law in a wide variety of problems. This includes using a free-body diagram to generate an equation (in 2D, that means one equation for x-,another one for y-) and use it to solve for acceleration. Alternatively, if the acceleration is known (given, or implied by the problem) then the equation can be used to deduce unknown forces.
... Use Newton's third law. (This means you recognize situations where it applies, you properly attribute forces to the correct object, and you get the signs of all force components correct)
... identify the "normal force" in problems, and use Newton's laws (2 and 3) to deduce the normal force in e.g. tilted tracks, or in situations with "stacked" objects.
... solve problems with weight (mg) and "apparent weight" (normal force when you are also accelerating up or down)
... solve problems involving friction, including both kinetic friction and static friction.
... combine multiple forces acting at different angles (using basic vector addition)
Chapter 5 Circular Motion.
... know when the formula a = v^2/R (centripetal acceleration) is applicable (uniform circular motion, steady speed)
... solve basic Newton's 2nd law problems when an object is moving with uniform circulation motion, which includes setting up a free-body diagram, writing down, and solving Newton's second law.
Update: That's it for Sp 14 2nd midterm - We will cut off the 2nd midterm here, so the rest (above) will be for the THIRD midterm. There will NOT be questions on anything after Giancoli material in section 5-2 for the 2nd midterm
__________________________________________________________________________________________________
The class did great overall on exam 1, nicely done! Here is the histogram of "raw" scores (# correct out of 21 questions):
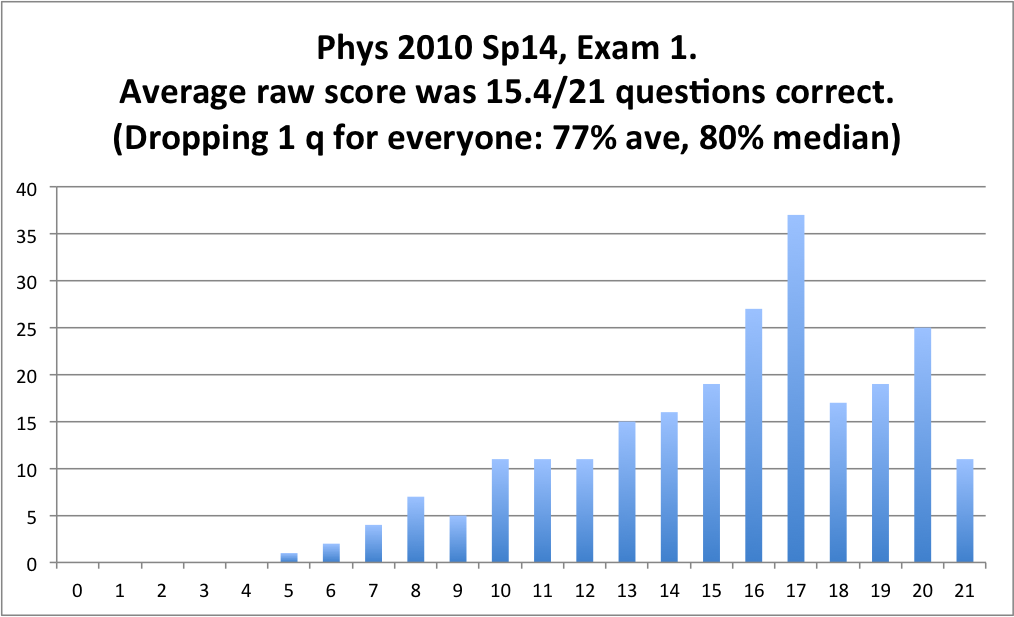
(Note: To convert this exam to a percent, we divided your score by 20, not 21. That is the same as dropping one missed question. Except if you got a perfect score on the Multiple Choice, (congrats!) - then we didn't drop anything, and just computed your score in the usual way, 100%)
- The average score (computed this way) was 77%, super!
- The median was just below 80% (That means half the class scored above 80%).
- The "Standard Deviation" was 18%.
- We don't assign letter grades to exams. Only your total combined course score matters for your final grade! (See below)
- About 1/3 of the class scored above 90%, that's really fantastic, congrats.
If you are really unhappy about your score, please read this page. It has suggestions for concrete steps you might take. Also note the "resources" link at the top right of our course pages. After reading these, if you'd like to come see Prof. Pollock or Prof Uzdensky, check out the "Help Room hours" link, or the "contacts" link, or just email us, or visit before/after class.
If you have serious concerns about the exam scoring, contact Steven.Pollock (at) Colorado.edu. Note that I keep all bubble sheets (which ALWAYS take precedence over what you circled on the exam)
By the way, we don't assign letter grades to exams. Only your total course score determines your grade. See the syllabus for the weights of various course components. Here is a distribution of "total course score" so far (To compute this, I assumed your future exam scores will match this first one, your future homeworks will match the first few, etc. It's still early in the term, that's the best I can do) The class is doing great, lots of A's and B's (way more than half the class so far) Keep it up!
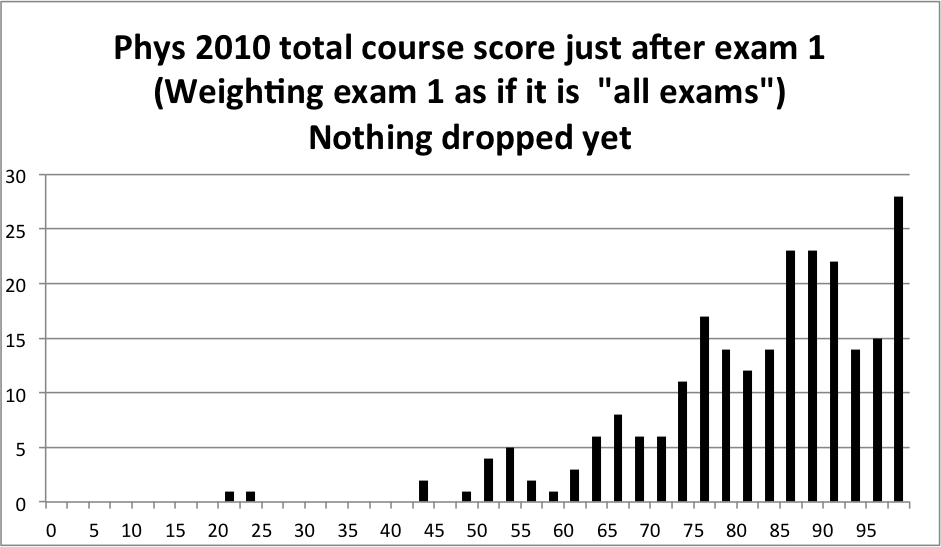
OLDER: STUDY INFORMATION FOR EXAM 1:
NEW: 2 PRACTICE EXAMS are now posted on our D2L page. On the "Course Home" page, look for the "content browser" window and go to "exams". You certainly do NOT have to do these, they are just there if you want some extra practice. (They are from two different instructors, with somewhat different styles from ours.)
NEW: There will be an evening review session 5-6:30 PM in G125 on Tues Feb 4. It will be very informal, nothing planned, just a time/space to ask questions. (Most likely we will go over the practice test questions, that's what usually ends up happening!)
TA Rosemary Wulf will likely run this.
The first midterm covers material from the course through the week before the exam (Jan 31):
Introduction, units/dimensions, 1-dimensional kinematics, and the basic math of vectors.
This includes anything covered in lecture, posted lecture notes, recitation/lab activities weeks 1-4, CAPA 1-3, Written Homeworks 1-2, or Giancoli Ch. 1, 2, and 3.1- 3.4, all fair game!
Other review options: read the text! Look for the Conceptual Examples scattered througout. Your goal in studying should be to keep trying FRESH problems, it doesn't do much good to try to memorize/repeat old ones. Look at the "Questions" at the end of each chapter (These come before the "Problems", which tend to be more computational. The exam will be a mix, but I would say slightly more "concept question-like" than "computational" on the whole)
Check out the Giancoli 5th Edition Website, he has nice sample problems and there are practice tests there too (with answers!) Look e.g. for the "MCAT practice problems", those are often decent.
Expect to see questions you have never seen before (we do not repeat problems we've already asked you!) but they will be similar to what you work on in clicker questions, recitation/labs, text examples, and the homeworks. We want you to show off your conceptual and computational/problem-solving skills, we're interested in your understanding of the physics, we are not interested in memorization or plug-n-chug behaviour or rote procedures.
For the first exam, here are some examples of our learning goals.
Each bullet below should be preceeded by You are expected to....
Ch 1: Introduction
... use the correct number of significant digits in calculations
... convert from one unit to another, even with complicated derived units like m/s^2 to inches/month^2, for instance. (Note that we do not expect you to memorize or waste crib-sheet space on constants and conversions. We will give you anything you need except perhaps the most elementary facts, like 12 inches in a foot)
... know the basic metric prefixes (specifically milli, centi, kilo, and mega) (Any others we would likely define for you)
... be able to work with SI metric units (m, s, and kg so far), including knowing "typical numbers" (what we call the order of magnitude) of everyday physics quantities. (Like roughly how big a person is (order 1-2 metres), or how fast you walk (1-2 m/s), etc)
... know the difference between units (e.g. meters) and dimensions (e.g. length)
... be able to calculate the dimensions of physical quantities from formulas, and use this to decide if formulas are possible or impossible.
... be able to read and use scientific notation in expressing large or small quantities, and doing basic manipulations (like multiplication or division) with it.
Ch 2: Kinematics
... know the difference between distance and displacement, and be able to compute either given a story, graph, or formula.
... choose a coordinate system, and realize what changes when you "flip" the choice of positive direction.
... know the difference between speed and velocity, and be able to find either given a story, graph or formula
... know the difference between average and instantaneous quantities, and be able to use a graph, equation, or numbers to qualitatively estimate either one (e.g. given a simple x versus t graph, you should be able to compute average velocity over any time interval, and instantaneous velocity at any point)
... know the definition of acceleration and be able to extra it from stories, graphs, or formulas
... extract the sign of velocity and acceleration from graphical means (e.g. "seeing" how the slope of the velocity vs time graph tells you the sign of acceleration)
... be able to "tell the story" from a graph or formula, so you can describe what is physically happening.(Or vice versa, be able to go from a story to a sketch or formula)
... solve basic "word problems" involving the 4 central "constant acceleration" 1-D kinematics equations (see Giancoli section 2.5) This includes being able to choose a coordinate system (or work in one that WE choose for you, which might be backwards from what you normally use), decide which equation is the appropriate one to use in a given situation, do basic algebra to manipulate those equations, and interpret all the symbols in the equations.
... manipulate these 1D equations with numbers but also WITHOUT numbers (purely symbolically)
... solve simple "multi-step" 1-D kinematics problems, where e.g. the "final" velocity from one part of the problem becomes the "initial" velocity in the next part. (Graphically, this means situations which are no longer constant acceleration, but are "piecewise" constant acceleration: so that each time period has constant acceleration)
... recognize when problems involve "freefall", and thus solve constant acceleration problems involving the acceleration of gravity.
... avoid common misconceptions as described in the text (e.g. avoiding the misconception that acceleration and velocity must always be in the same direction, avoiding the misconception that acceleration is zero at the top of a freefall trajectory, avoiding the misconception that a = v/t rather than delta v/delta t, avoiding the misconception that if you know velocity as a function of time, then the motion must start at x=0 (it could start anywhere, unless you are explicitly told!), avoiding the misconception that g is negative (it is definited to be+9.8 m/s^2: the sign of acceleration in a FORMULA depends on your choice of coordinate system)
... solve problems in 1D even if they are "tilted" (like objects on an air track)
... move comfortably back and forth between graphs of (x vs t) (v vs t) and (a vs t)
... intepret the above graphs to be able to describe the physics, or vice versa (e.g. sketching a graph given a description of the motion)
Chapter 3: Vectors. (Below is for exam 1 only: the remainder of Ch 3 will be on the 2nd midterm)
... distinguish between a vector and a scalar quantity, and decide whether some given physical quantity is one or the other
... be able to compute the components of a vector given a graphical picture of the arrow, and vice-versa: find the angle and length of a vector given the two components.
... know the basic geometrical trig identities (definitions of sin, cos, and tan) and be able to work your calculator to take those functions or the "inverses" to find angles.
... add vectors graphically
... add vectors using the method of components
... subtract vectors graphically, or using the method of components.
... multiply vectors by a scalar (graphically, or with components)
___________________________________________________________________________________________________
Please consider "power posing" before your next exam!