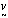 or
or
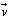 .
They are generally drawn as an arrow,
.
They are generally drawn as an arrow,
 ,
but the location really doesn't matter, only the magnitude and the
direction. The magnitude is given symbolically by
,
but the location really doesn't matter, only the magnitude and the
direction. The magnitude is given symbolically by
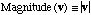 .
.
(or "Mathematical Methods for Physics")
Course Introduction:
* In a nutshell, the purpose of Physics 2140 is to teach you some basic tools useful in any physical sciences.
* I will assume you all know some basic calculus, trig, standard functions (log, exp, etc)...
* Mathematics is the LANGUAGE of physics! It is critical for physics majors (and engineers, chemists...) to master certain mathematical techniques which are at the heart of topics to be studied in jr and sr level classes. This material will usually be assumed in (advanced) E+M, mechanics, Quantum, stat mech, engineering.
* Mathematica (MMA) has been chosen as the computer language of choice for this course - it could as easily have been Maple, or C, or Fortran..., but MMA is fairly easy to learn, and yet quite powerful. It is available on most platforms, and is used by lots of physicists. Most of the skills and tricks you learn here will prove useful in future courses. They will also be transferable, to a certain extent, to other computer environments you'll encounter in the future. MMA will not be taught in lectures, but through "guided teaching" in the h.w.'s
* Boas is an excellent text, but chooses an odd sequence of topics. We'll "wind" through it in a sequence more appropriate for your needs.
* There is way too much in Boas for 1 semester, but don't forget about the book in future years - it's a good resource!
* There are plenty of other topics in mathematical physics that we really should cover in 2140, but simply don't have the time for. (Linear algebra, complex analysis, chaos, the list is long!) My philosophy is that it is better to have a solid grounding in the more frequently required math methods. You can always learn more in math classes, or on your own in the future.
* The math topics we will cover are all directly useful for physics, and we'll try to keep sight of this. The topics are diverse enough that the flow may not always seem obvious to you. When in doubt, ask me! You'll be surprised how many different places each of these topics ends up getting used in future physics classes.
Bottom line - there are some mathematical tools you will need a lot in physics, and this course aims to teach them to you!
Section 1 (Aug 28 - Sep 6) VECTORS
Vectors have magnitude and direction. Symbolized by v or
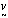 or
or
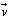 .
They are generally drawn as an arrow,
.
They are generally drawn as an arrow,
 ,
but the location really doesn't matter, only the magnitude and the
direction. The magnitude is given symbolically by
,
but the location really doesn't matter, only the magnitude and the
direction. The magnitude is given symbolically by
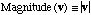 .
.
Which is a vector? Mass, weight,
temperature, temperature gradient, force, velocity, speed, pressure, area...
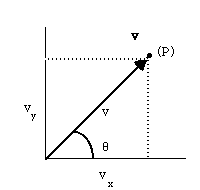
In 2 dimensions, one length and one angle suffice. Sometimes we represent this vector by specifying, in some way, a single point, P, in the plane. (So, we implicitly assume the "tail" of the vector is at the origin, and the "head" is at the point P.)
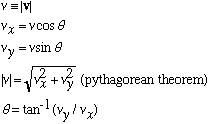
In this example, the vector V can be represented in Cartesian coordinates as
V = (Vx,Vy).
Or, in polar coordinates, it would be represented by
V = (v,theta).
But, I don't have to choose a coordinate system. A vector is the arrow, independent of which axes we may choose.
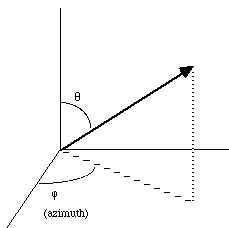
In three dimensions, we need a length and two angles.
Again, we often characterize a vector by the coordinates of its tip.
With respect to these chosen (arbitrary) axes, that would be given by:
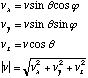
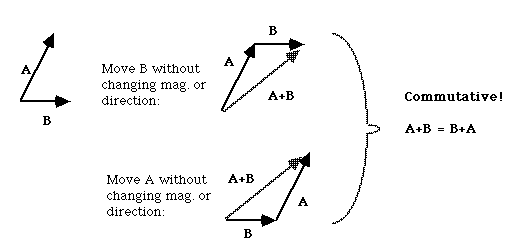
Vectors can be added - put the tail to the tip, graphically:
Components of a vector behave simply:
A+B=C means Ax + Bx = Cx and Ay+By=Cy
Vectors can be multiplied by a constant (i.e. a scalar, a number)
n A is parallel to A, but n times larger, so
nA = (nAx , nAy) in Cartesian, and nA = (n|A| , theta) in polar coordinates.
(You cannot add a vector to a scalar. But you can multiply or divide by a scalar.)
If n=-1, you get -A, the mirror (reverse) of A. So, you can subtract vectors, because A-B = A+(-B):
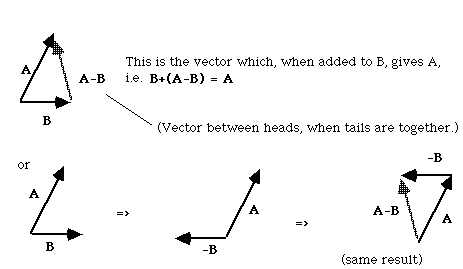
You can add many vectors, not just 2:
v1 = displacement from bed to b'kfast table.
v2 = displacement from table to G-125
v3 = displacement from G-125 to UMC
v4 = displacement from UMC to study hall
v5 = displacement from study hall to dinner.
v6 = displacement from dinner to bed
v = v1+v2+v3+v4+v5+v6 = 0
If v1 = 0, you're on a diet
If v1 and v5 = 0, you're starving to death
If v2 = 0, you're flunking...
An example: (this is an old proof from geometry) Prove that the diagonals of a parallelogram bisect each other.
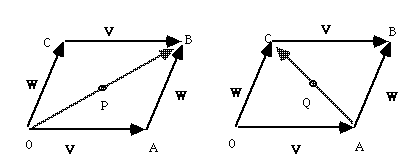
Let P be the bisector of this Let Q be the bisector of the
diagonal: OP = 0.5 OB other diagonal: AQ = 0.5 AC
So OP = 0.5(V+W) and
OQ = V + AQ
= V+0.5 AC
= V+0.5(W-V)
= 0.5 (W+V)
= 0.5 (V+W)
Which means that OP = OQ, so P and Q are the same point, i.e. the intersection of the diagonals bisects each of them. QED
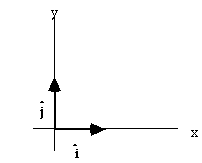
It is convenient to write vectors as "linear combinations" (sums) of chosen
unit vectors. (In fact, I have already been sort of sneakily doing this, when I wrote the vector explicitly in Cartesian coordinates) A unit vector always has length 1, and (usually) they are chosen to be perpendicular to one another. (They get written with a hat ^ on top)
 so
so
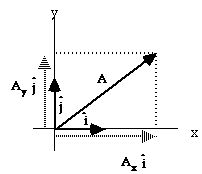
So, any vector A can be written as
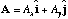 .
This is formally a representation of A in terms of its Cartesian
components and Cartesian unit vectors, i and j. Adding vectors is
easy when we have the components:
.
This is formally a representation of A in terms of its Cartesian
components and Cartesian unit vectors, i and j. Adding vectors is
easy when we have the components:
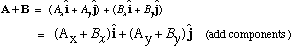
I will often use interchangeably different notations:

In this way, I can also write e.g.
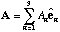
A unit vector in the direction of A can be easily constructed, it is
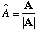 .
.
Dot Product: A.B is a scalar, a number.
A.B = |A| |B| cos [[theta]], where [[theta]] is the angle between the vectors A and B,
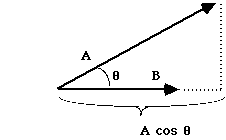
So if B is a unit vector, then A.B = |A|cos[[theta]], which is the component of A in the B direction.
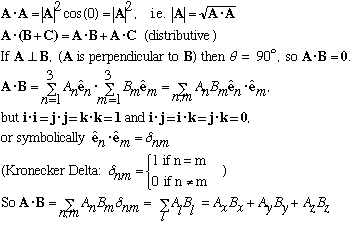
Here is the Next lecture
Back to the list of lectures