

Example:

To find the components of a vector, use e.g.

If A // B (i.e. if A is parallel to B) then all the components must be proportional Ax/Bx = Ay/By = Az/Bz. (And, if Bx=0 then Ax=0 too, etc.)
Physics Examples:
(1) Work = F . dx (Force . displacement). If a force acts through a displacement, dx, then the force only does a work equal to dW = F . dx = |F| |dr| cos(theta). So, if the force is perp. to dr, like, e.g. charged particle moving in a uniform B-field, where F=qv x B = q (dr/dt) x B, then dW = 0, and the force does no work.
(2) If mu = I A, mu is the magnetic moment of a current loop (area A).
And then the energy of that loop in a magnetic field B is E = -mu.B
Cross product also called "vector product". A x B is now another vector.
It has a magnitude: |A x B| = |A| |B| sin[[theta]] , and a direction, which is perpendicular to BOTH A and B, oriented using a "right hand rule".

Note: A x B = - B x A Cross products are NOT commutative!
If A is parallel (or antiparallel) to B, then A x B = 0. This also automatically means that A x A = 0.
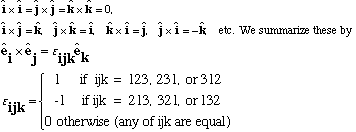
(= Levi-Civita symbol, or "anti-symmetric tensor")
Also, cross products are distributive, A x (B + C) = A x B + A x C, so writing A = Ax i + Ay j + Az k and B = Bx i + By j + Bz k, we can use the distributive property to compute A x B,

(Note the funny sign on the middle term!)
Digression: Determinants of Matrices. Given a 2x2 matrix, M,

This is called "expanding in cofactors". A cofactor of an element, aij in a matrix (in row i, column j) is (-1)^(i+j) dij, where d is the determinant formed by deleting row i, column j from the original matrix a.
You can expand any row, or column, (I chose the first row in the above example) Some factoids about determinants:
* If any row (or column) is all 0's, then the determinant is 0.
* If any 2 rows (or columns) are proportional, det = 0.
* If any 2 rows (or columns) are switched, determinant flips sign.
(There are many more such facts!)
Example:

Some physics uses:
(1) Torque about a point, t = r x F (torque is force x "lever arm"). The direction of the torque tells you how the object wants to rotate. (This is a convention..)

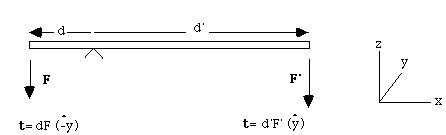
Note that the torque is 0 if (1) force is applied right at the origin (r = 0),
or (2) if force is parallel to r, since then theta = 0 (so sin(theta) = 0)
Angular velocity is a vector representing a rotating body, w:

(Makes sense, P is moving in a circle, speed = w r.)
Here is the Next lecture