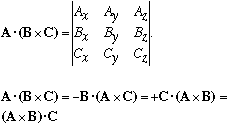
A.(B x C). This is a scalar (a number). By writing out B x C as a determinant, and then dotting with A, you can immediately see
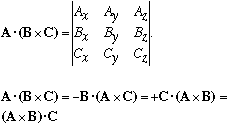
(These come from the fact that switching a pair of rows in a determinant gives a factor of -1. So, note that it really doesn't matter where you put the dot, and where the x.)
This triple scalar product has a direct geometrical interpretation:

Build a parallelepiped from
A, B, and C as shown. Then,
|B x C| = Area of base (because B C sin [[theta]] = base x height)
So the volume is
(area of base) x height
= |B x C| |A| cos j
= A . (B x C) . So, volume= |triple scalar product!|
Physics Application of triple scalar product:
The torque about a POINT is r x F. But, what is the torque about the line L?
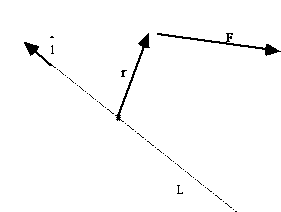
I claim it will be
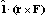
(Note 1st, if L is perp to the plane of r and F, then the dot product gives
|r x F|, which is just what we'd expect.)
Let l define the z axis. (Think of a door hinged along the z axis).:
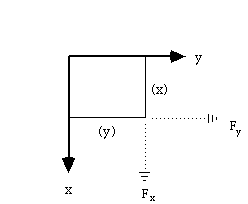
We want the torque of F about this z axis. So, any component of F along z doesn't help! Remaining torque is +x Fy - y Fx.
But,
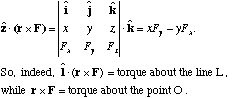
TRIPLE VECTOR PRODUCT: A x (B x C), a vector.
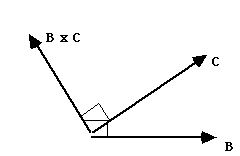
Now, A x (B x C) is perp. to (B x C). From the picture, we see that it must then lie in the same place as B and C do. SO, it must be some combination, aB+bC. We can find these coefficients by brute force, writing out (B x C) in components, then crossing A. The result is
A x (B x C) = B (A.C) - C (A.B)
This is the "Back-Cab" rule of triple products. The triple product is a combination of the two vectors in parentheses. Each coefficient is the dot product of the other two. The *middle* vector gets the plus sign.
(Note that the coefficients of B and C on the rhs are dot products, i.e just numbers!) Also note that (A x B) x C is different, it will be in the plane of A and B, not B and C. So, the order matters here!
Example: i x (i x j) = i (0) - j (1) = -j
This can be checked easily: i x j = k, and i x k = -j. (Check this yourself)
Q: What do you get when you cross an elephant with a grape?
A: |Elephant| |Grape| sin(theta)
Q: What do you get when you cross a grape with a mountain climber?
A: Nothing. You can't cross anything with a "scalar"
A Physics application of the triple product:
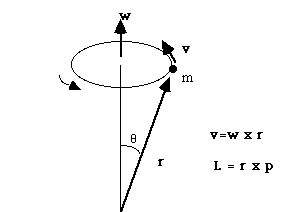
Angular momentum of a spinning particle, mass m, about the origin is
L = r x p = r x (m v). But recall, v = w x r, so, L = m r x (w x r)
Lines and Planes.
Think of a point (x,y,z) as defining a vector, r = x i + y j + z k.
Now we can think of a the vector between two points as the difference of the two position vectors:
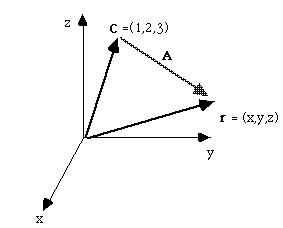
A = r - C. We can write it as (x-1, y-2, z-3), or as
(x-1)i +(y-2)j+(z-3)k. I've already been doing this, in fact! Now, think of a line:
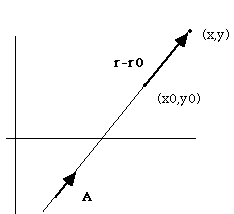
If the slope of this line is m, the equation for the line is
y-y0 = m(x-x0),
or y = y0+m(x-x0). If, instead of being given the slope and a point directly, we have instead been given the vector A = ai + b j, which tells us the direction of the line, and a single point (x0,y0) on the line, we can also write the equation:
r - r0 = (x-x0)i + (y-y0)j, which simply gives the vector from the point (x0,y0) to (x,y).
Looking at the picture, if (x,y) is to lie on the line, then this vector must be parallel to A, so as stated above, the components must be proportional, i.e. (x-x0)/a = (y-y0)/b. (Rewriting this, we get y=y0 + (b/a)(x-x0), back to our usual equation for a line).
Here is the