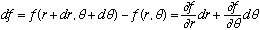
What is grad f, when f is given in terms of r, theta, (and phi?)
Recall the fundamental concept regarding gradients: for any scalar function f, the total differential df = grad f . dr
This is a vector equation, so it must hold in polar coords too!
Let's start in 2 dimensions:
f=f(r,theta), then
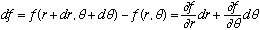
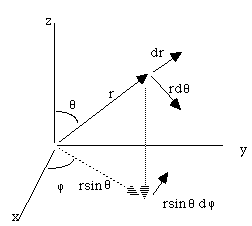
Now, what is dr in polar? Look at the picture:
,
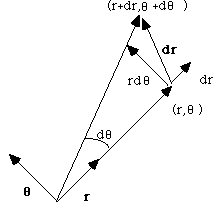
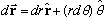Now, say grad f = A r +B [[theta]],
(A and B as yet unknown) =>
grad f . dr = A dr + Br d[[theta]]
= df
=
Which means
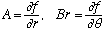
Putting this together gives us what we wanted, the gradient in polar:
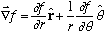
I can think of this in a slightly different way, (and move to 3-d too)
Imagine looking at df/ds as you move in r,theta, and phi
directions. When you move in the r direction,
If you move in the r direction,
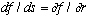
But in the theta direction,
Why? Because the path length,
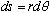(look at the picture)
Similarly, in the phi direction,
,
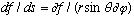because
in this direction,
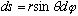
Now, grad f .r should = df/ds when you move in the r direction.
And grad f .theta = df/ds, when you move in the theta direction,
etc. So, we can just read off the spherical coordinate equation:
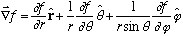
N.B. it is not trivial to work out the div and curl from this formula
just yet (we'll need to learn more first). But here is the result: if a vector
field in polar coordinates is given by
,
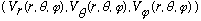then
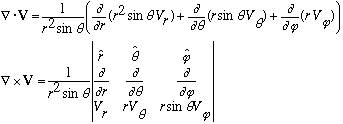
On a related note, for line integrals, its useful to have formulae for the element of line length ds in other coordinates:
ds2=dx2+dy2+dz2 (rect)
(spherical)
and volume elements are
dV = dx dy dz (rect)
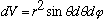(spherical)
We have developed this weird thing, del or
.
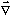It's an operator, but we have been essentially treating it like a vector. So,
e.g. we can form
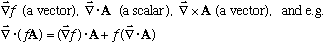
(Careful! The grad operator only operates on f in the 1st term on the right hand side!) Similarly, we can define the Laplacian of f,
In general, plain old vector rules continue to apply, but you must keep care of what the del operates on! E.g, As in the BAC-CAB rule:
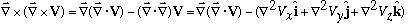
(see Boas p. 296 for more such relations!)
Here is the Next lecture