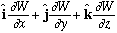
Why were the line integrals all different in the 1st example, same in second? Is there something special about the integrand?
Physically, if the work is the same for all paths, we call the force "conservative" (we'll see why soon). Put another way, F is conservative if the integral of F.dr depends only on the endpoints of the path, and not the details of the path itself. If it is path dependent, we call it non-conservative. (Think of friction - dragging something costs more work than lifting and carying. So, friction is nonconservative)
How can we tell, mathematically? First- here's the ANSWER!:
If (a) I can write F = grad W =
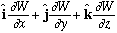
for some function W(x,y,z),
OR (b) if curl F = 0
THEN F is conservative, and the integral of F.dr is independent of path.
Why should this be? We'll talk more about it later, but observe that
if (a) is true, then
But the object in parentheses after i on the right hand side is always 0 (crossed partials are equal), same for the other two terms, so at least if (a) is true then (b) is clearly automatically true. (We'll show the reverse later!) Next, if (a) is true, then
F.dr = (grad W).dr=
,
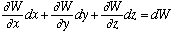which means
,
i.e. the integral is path independent. (Integral is of a "total derivative", or
an "exact differential", or a "total differential", dW= (grad
W).dr. It tells the total change in a function as you move from one
point to another. (See picture, Boas p.152). So, if F.dr is a total
differential, then F is conservative, because the integral is path
independent. Now, looking back at my two examples:
F=2xy i + 2x2j, so
,
so this F is not conservative, and that's why the integral was path
dependent.
Second example, F wasn't given, we just had
,
but this is equivalent to F = (x+2y)i+2xj+0k, and
then
,
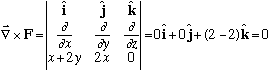i.e. it is conservative, and indeed, our line integrals were all equal.
We just showed that if F = grad W, then the integral of F.dr from A to B is W(B)-W(a). In mechanics, W is called the work done by F. This is also the negative of the potential energy, F = -grad V.
Ex: Gravity. F =-mg z, and V = mgz = potential energy.
The work done by gravity when you lift an object is the integral of F.dz, which is -mg (Delta z).
The change in potential energy is Delta(V) which is just +mg (Delta z). So, the integral of F.dr is W(B)-W(A)=-(V(B)-V(A))
The total change in energy,
Delta E = Work + Delta(potential energy) =
-mg (Delta z) + mg (Delta z) = 0.
I.e., the total energy is conserved - hence, a conservative force!
What good is this function W? Lots! If you know that curl F=0, then there must be such a function W, (unique to within a constant) (we haven't proven this yet!) such that F=grad W. We have shown this means the integral of F.dr (which in general is a hard integral!) equals W(B)-W(A), which in general is just subtracting 2 numbers - easy!
Example: F = -k r = -k (xi +yj + zk), so
,
so F is conservative.
Now we ask, what is V such that F = -grad V? Sometimes you can just "guess", and there are various ways to get it, but here's a technique that always works:
Since the integral of F.dr is independent of path, and =-(V(B)-V(A)),
we can just pick an arbitrary point for A=(x0,y0,z0), let B = (x',y',z'), and choose any path we like (they're all the same) to do the integral, which will always give us -(V(x',y',z') - V(x0,y0,z0)).
(The latter term is just a number, in fact, an irrelevant constant, because adding any constant to V has no effect on F = -grad V)
In this example,
.
Let A=(0,0,0), B=(x',y',z'), and let the path be as shown in this figure:
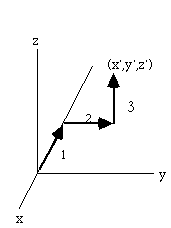
Path 1 gives dy=0, dz=0, and
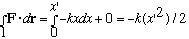
Path 2 gives dx=0, dz=0, and
Path 3 gives -k z'2/2,
so the integral of F.dr from A to B is -(k/2) (x'2+y'2+z'2)
Thus, V(x,y,z) = +(k/2)(x2+y2+z2) = (k/2) r2.
Check! -grad V = -k(xi + yj + zk) = -k r, indeed!
We could also have integrated out along a radius vector (spherical coords), then
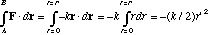(same).
Note: It is not true that |dA| = d|A|, in general, because you might be changing direction as well as length!
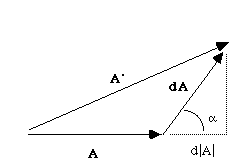
A.dA
= |A| |dA| cos(alpha)
= |A| d|A|
So, it is true that for the position vector,
r.dr
= |r| d|r|
= r dr,
which I used above. (If you don't like this proof, note:
d(r.r) = 2r.dr = d(r2)=2r dr )
Even if you have no forces, but just a line integral, you can use the same ideas:
Ex: Is 2xy dx + x2dy an exact differential?
Soln: Think of it as coming from F=(2xyi + x2j), so that
curl F = (work it out!) (2x-2x)k = 0,
=> F is conservative, => F=gradW for some W, =>
F.dr = 2xydx +x2dy = gradW . dr = dW
So yes indeed, it is an exact differential. Next question - what is it a differential of? Try the same trick I used before, namely
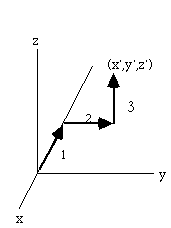
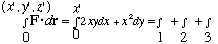
But on path 1, dy=dz=0, and y=0, giving 0.
path 2 gives dx=dz=0, x=x',
and path 3 gives dx=dy=0, (0 again) =>
,
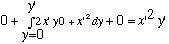W=x2y.
Check: dW = 2xy dx + x2dy, indeed!
More on the potential:
A review of what I've just said: If F is conservative, then we
can define a corresponding potential energy V(r) = -Work done by
F on a body moving from a reference point r0 to r, =
.
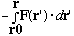Since F is conservative, this integral has a single well defined value
for any r.
(r0 is arbitrary. It corresponds to a little ambiguity in V, but we generally only care about Delta V, so it doesn't matter.)
For gravity near earth, V = mgz - mg0 (reference point is the surface), but far from earth, we use V = -GMm/r (reference point is at infinity).
Why the minus sign? It's a convention! But a useful one: think about throwing up a ball. As it goes down, gravity does + work. As it goes up, gravity does - work (steals KE).
So, defining Delta V as -Work means that as it goes up, (losing KE), it gains PE (with this sign convention!), so the total energy is conserved.
Bottom line: V is an integral of F, and as you'd expect, F is a "derivative" of V. Since this is 3-D, it's a special kind of derivative - the gradient. We showed before, that if F=-grad V, then F is conservative. Let's now go the other way, i.e. show that if F is conservative, then there must be a V such that F = -grad V:
Suppose F is conservative and simply choose
Now let r be close to r0=>
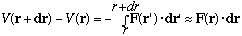
But, dV == V(r+dr)-V(r) = grad V . dr (from our definition of the gradient), so
F.dr = -(grad V)dr.
Does this show F=-grad V? Not quite! A.B=0 doesn't mean A=0. But, dr is arbitrary. It can be in any direction. This is important!
E.g, dr = a i, and dr = b j, both give 0. Which means
Fx=(grad V)x, and Fy=(grad V)y, so indeed, F=-grad V.
Example, from electrostatics:
F=qE.
P.E. = q V
F = -grad (P.E.)
qE = -gradq V => E = -grad V.
For a single charge, V = kQ/r, E = -grad V =
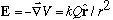
(we'll derive the last step soon!)