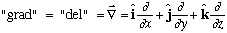It's a weird thing!! It doesn't mean anything by itself, only when it operates
on a function. So,Given f = x2-y2z = 0 (this defines some curvy surface):
What is the tangent plane to the surface at (1,1,1)?
What is a normal line through (1,1,1)?
Sol'n: grad f = (2x, -2yz, -y2), grad f|(1,1,1) = (2,-2,-1)
So, the normal line must have a direction (2,-2,-1), and runs through (1,1,1), i.e.
(x,y,z) - (1,1,1) = (2,-2,-1) t (parametric form), or
(x-1)/2 = (y-1)/(-2) = 1-z (symmetric form)
The tangent plane (see notes, earlier!) can be read off too, since we know the normal to it:
2(x-1) - 2(y-1) - (z-1) = 0
We will be using "del" in many ways this course, so let me generalize, and define the "del" or "gradient" operator as
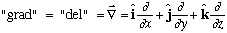It's a weird thing!! It doesn't mean anything by itself, only when it operates
on a function. So,
e.g.
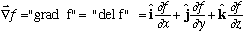(as we had) But it can now operate on something else besides a scalar function!
E.g., if v(x,y,z) = vx(x,y,z)i + vyj + vzk, then
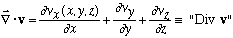(a scalar function!), and
(= curl v, a vector function). We'll be seeing much more of these soon!
Line Integrals.
Recall from mechanics that work = F.displacement, i.e. dW = F. dr.
What if the particle moves along some path in space, acted on by a force? What is the total work done on it?
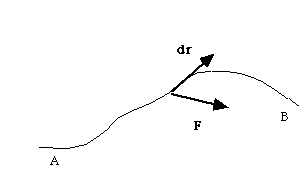
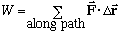
But, we can't work this out unless we know exactly the path taken from A to B. (unless F is very special, as we shall see later)
Lines are given by sets of equations (recall the formulae for straight lines), or as a parametric equation. In any case, (x,y,z) on a line can always be expressed as functions of a single variable, s. (You might think of s as representing "path length from A", but it doesn't have to) So, along the curve, F(x,y,z) and dr = i dx + j dy + k dz are both functions of this single variable, s. So, our sum along the path of
F . Delta r becomes
.
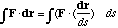The lhs is a "line integral", which winds through space, but the rhs is in fact
a plain old integral. This is no longer some weird 3-d integral, but an
ordinary one-dimensional integral of a scalar function. (Note that dr/ds
is the equation for a tangent vector to the curve)
Example:
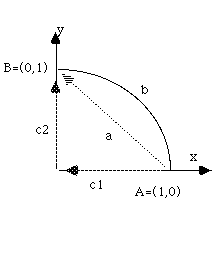
Suppose F= (2xy) i + 2x2 j. Let's calculate the work done on a particle going from A to B along different paths.
Path a is the line y=1-x
Path b is a semicircle
Path c is the two straight lines, going first in along x, then up along y.
Path a) F.dr = Fx dx + Fy dy = (2xy) dx + 2x2dy.
But y is a function of x, so we can re-express the whole integrand in terms of x alone! So, F.dr = 2x(1-x) dx + 2x2 (-dx)
(Note: y = 1-x so dy = -dx)
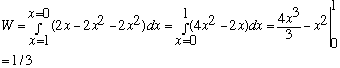
What if we had eliminated x instead of y? x = 1-y, dx = -dy, gives the same result (try it!)
b) For this semicircle, instead of using either x, or y as the variable, use the angle theta! So, x=cos(theta), y=sin(theta), and the path runs from theta=0 to theta=Pi/2. Also,
dx = -sin(theta) d(theta), and
dy = cos(theta) d(theta). So
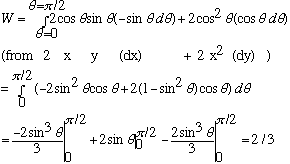
c) Path= c1+c2? Along the 1st part, y=0, dy = 0, so
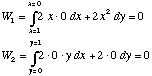
So W = W1+W2 = 0.
(A different answer each time!)
One more example:
This time, it's not necessarily a work problem. Just a pure line integral:
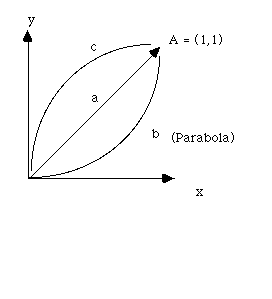
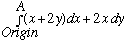
Path a is y=x
Path b is y=x2
Path c is y=t2, x=t3 (parametric)
Path a) y=x (let's eliminate y), so dy = dx
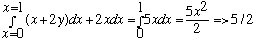
Path b) y=x2, so dy = 2x dx, integral is
Path c) x=t3, y=t2, so dx = 3t2dt, and dy = 2t dt, so integral is
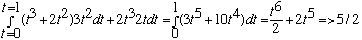
This time, same answer each time. Is this a coincidence? We shall see...
Here is the Next lecture