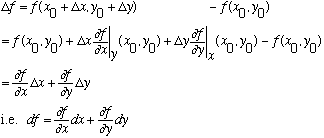
Another way to describe partial derivatives: start at f=f(x0,y0), and move to some point (x0+dx, y0+dy), what is the change in f?
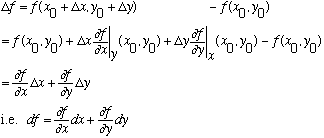
This important result tells the total change in f as we move by dx and dy. (Should look at Boas Ch. 4 if this isn't familiar)
Directional Derivative: The gradient.
Motivation: In 1-D, if a fn depends on x, then the change in the fn as you move
along x is unique, and easy to define: df/dx. What if a function depends on 2
variables? What is the change in f as you move? Put another way, "how steep is
the hill" at the point (x,y)? This is ambiguous! We saw part of the answer from
partial derivatives:
,
if you move purely in the i or j directions. But, what if we
move along some other direction?
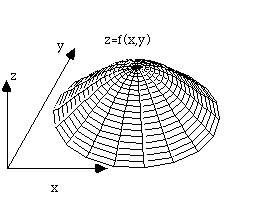
That is, if we move along (above) some vector ds in the x,y, plane, we would like to know the change df, or perhaps df/ds. Furthermore, it seems obvious that at any point, there must be some direction we can move which changes f the most rapidly.
The gradient will solve all our problems!
Extending to functions of 3 variables is no problem, just a lot harder to draw. E.g, if the temperature T(x,y,z) is known, we might like to know (a) How rapid is the change in temperature if we move in some arbitrary direction? and (b) which direction should we move to (cool off) (heat up) the fastest?
For the first of these: given a function f(x,y,z) (could be temperature, height of a hill, electrical potential, etc), we want to find df/ds
at SOME arbitrary point (x0,y0,z0), as we move in SOME fixed direction u. (let u be a unit vector)
Suppose we move a distance ds, in the u direction. How much does f change?
df = f(x,y,z) - f(x0,y0,z0)
But note from the picture that
x=x0+ux ds (=x0+dx)
y=y0+uy ds (=y0+dy)
z=z0+uz ds (=z0+dz)
( from (x,y,z) - (x0,y0,z0) = u ds)
So *just* as I had before (except now with 3 v'bles)
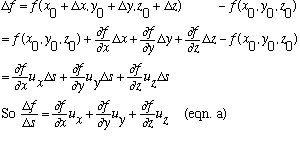
(If you like, this all follows from expression for df earlier, directly)
We can write this last expression as a dot product of the vector u with something. The definition of that something (the gradient of f):
The latter expression is the "directional derivative" of f in the u direction. We can also take the more general expression, from the line before the last one in (a), and write the total differential df, for a differential displacement dr = u ds, as:
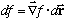
This formula is really the key concept concerning gradients. (The directional derivative follows by dividing out the length ds = |dr|.)
Some things to note about the directional derivative:
Which direction u should I move to maximize df/ds? I.e., which way is
"up the hill"? Well,
,
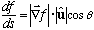where theta must be the angle between u and grad f. But, |u| is
always 1, and the magnitude of grad f at some point has some value, so to make
df/ds as big as possible, I should make cos(theta)=1, i.e. theta=0. So this
means, if the direction of u is the same as the direction of
,
that's the way to go to maximize df/ds. And, if I go that way, df/ds = |grad
f|.
First example:
T(x,y,z) = xz + y2.
What is the directional derivative of T in the direction A = (2, -2, 1) at the origin? How about at the point (1, 2, 3)?
Soln: First, find u, the unit vector in the direction we want. So in this case, u = A / |A| = (2, -2, 1)/(3).
Then, grad T = (zi + 2yj + xk) = (z, 2y, x)
So, grad T at the origin is (0,0,0)
grad T at (1,2,3) is (3,4,1)
Finally, dT/ds = grad T . u = 0 (at the origin), but
=(6-8+1)/3 = -1/3 (at (1,2,3))
Next example: Given that same temp distribution, T, if you're sitting at the point (1,2,3), which direction must you go to see the most rapid temperature change? How fast is the change in that direction?
Sol'n: grad f = (z, 2y, x)
So, grad f|(1,2,3) = (3,4,1)
The temperature changes the fastest in the direction 3i +4j+k. The rate of change in that direction is
dT/ds = |grad f| = sqrt(9+16+1) = sqrt(26)
The temperate decreases fastest when theta=180, i.e. when u points opposite the gradient, in this last example that would be in the direction (-3,-4,-1). At that point, dT/ds =-sqrt(26)
(Heat flows from hot to cold, i.e. in the direction of -grad T)
Next note: If f(x,y,z) has a contour surface, f=constant, and u is tangent to that surface at some point (x0,y0,z0), then df/ds=0 along the surface (since f=constant!) Which means grad f . u = 0 there. Rephrasing: grad f is perpendicular to the surface f = constant. Also, since |grad f| is the value of the directional derivative perp to the surface, it is often called the "normal derivative", and is sometimes written df/dn. So, the direction of maximum rate of change is perp. to the equipotential (f=constant). E.g, on a hill, grad z always points up the steepest way, and this is always perpendicular to contour lines.
Another example:
T = c(x2+y2+z2) (which is also c r2 in polar coordinates)
What is the directional derivative of T at the point (2, 2, 1) in the directions (1) U1 = (2,4,4),
(2) U2 =10i,
(3) U3 = (2,2,1)
Sol'n: grad T = c(2x i + 2y j + 2z k ) (which, b.t.w. = 2 c r)
At the point (2,2,1), grad T|(2,2,1) = c(4,4,2)
Making my directions unit vectors:
u1 = (2,4,4)/sqrt(4+16+16) = (1/3, 2/3, 2/3)
u2 = (10,0,0)/sqrt(100) = (1,0,0), i.e. i
u3 = (2,2,1)/sqrt(4+4+1) = (2/3, 2/3, 1/3)
Now, dT/ds =
(1) grad T . u1 = c (4,4,2) . (1/3, 2/3, 2/3) = 16 c/3
(2) c(4,4,2) . (1,0,0) = 12 c/3
(3) c(4,4,2) . (2/3, 2/3, 1/3) = 18 c/3
N.B. T = cr2, so equipotentials are spheres r=constant. We expect the gradient to point normal to r=constant, i.e. in the r direction. It does! grad T = 2 c r.
Note also, dT/ds should be maximized when u is in the r direction. (Certainly, of the 3 examples above, the third (which has u pointing in the r direction) is the largest.
Finally, dT/ds should be the same as |grad T| if u is in the direction of the gradient, i.e. in the r direction, i.e. dT/dr = d(c r2)/dr = 2 c r,
which is correct.
Here is the Next lecture