Vector Calculus I: Directional Derivatives
In calculus, we learned about the rate of change of a scalar function. E.g., if you know x(t) (position as a fn of time), the velocity is just dx/dt. Similarly, if you know a vector A(t), it has a derivative too:
dA/dt = i dAx/dt + j dAy/dt + k dAz/dt
This is also a vector:
Technically, dA/dt = lim(dt -> 0) (A(t+dt) - A(t)) / dt
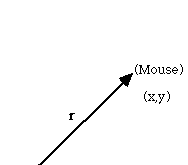
Imagine tracking the position of a mouse running around the room:
The position (x,y) is a function of time. So,
r = i x + j y = i x(t) + j y(t)
(changes with time, i.e. r = r(t))
r is the "position vector" or "vector coordinate". What is the velocity of the mouse? The x velocity is dx/dt, the y velocity is dy/dt =>
v = dr/dt = i dx/dt + j dy/dt
Acceleration a = d2r/dt2 = i d2x/dt2 + j d2y/dt2
You can take derivatives of products. (If you forget these rules, or don't believe them, just write everything out component by component!)
d(c A)/dt = (dc/dt) A + c dA/dt
d(A.B)/dt = A.dB/dt + (dA/dt) . B (order doesn't matter in either of these, because c A = A c, and A.B = B.A)
d(A x B)/dt = A x (dB/dt) + (dA/dt) x B
(order DOES matter, keep A and B in the same order!)
A classic example: circular motion, constant speed.
(remember a = v2/r?)
r2= r.r = constant (because we're moving in a circle)
v2=v.v = constant (because speed = |v|=constant, and v2=|v|2)
Differentiate each of these:
d(r.r)/dt = r. dr/dt + (dr/dt).r = 2 r.dr/dt = 0 => r . v = 0 (1)
d(v.v)/dt = 2 v dv/dt = 0 => v.a = 0 (2)
Differentiate (1) again, to get r.dv/dt + (dr/dt) . v = 0, i.e.
r.a + v2=0 (3)
Conclusions: from (1), r . v = 0, so velocity is perpendicular to position. (Makes sense for circular motion - this is a much easier proof than the one usually used in 1110. See fig. below)
From (2) v . a = 0, i.e. acceleration is perp to velocity (again makes sense)
and then r.a + v2=0, but r and a are both perp to v, which means r and a must be parallel (or antiparallel), since this is all 2-D. Which means (again from (3))
r . a = |r| |a| cos(theta) = -v2.
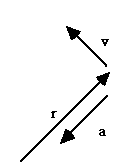
But I just argued that theta must be 0 or 180. Since the right side is negative, theta must be 180 to make the lhs negative too.
We conclude a is directed inwards (opposite of r), and also
-a r = -v2, i.e. a = v2/r
(These are all the facts you ever wanted to know about circular motion, just be differentiating a couple of vectors!)
How does all this work in polar coordinates?
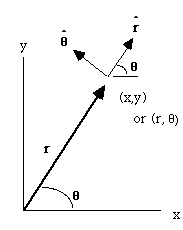
Now we must be careful, because
are changing, along with the particles position!
From the picture:
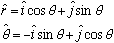
(convince yourself these equations are right!)
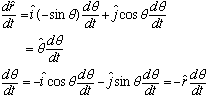
Ex: Suppose a particle's path is given by r(t) = constant,
(this is uniform circular motion, again!)
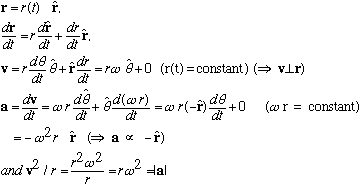
Same results as before! Bottom line: di/dt =0, but
,
so it's trickier to differentiate vectors when given in polar coords.
Vector Fields -
Description of a vector quantity which varies in space.
(A "scalar field" is a scalar quantity which varies in space)
Examples of scalar fields: Temperature in room, Potential energy near earth. Examples of vector fields: Electric field (see below), Force, Fluid velocity...
Vector fields are hard to draw!
(There is a value of the field at every point in a region of space)
E(x,y,t) = Ex(x,y,t)i+Ey(x,y,t)j
It's slightly easier to draw scalar fields defined in 2-D, by using the third dimension to show the *value* of the field. E.g, the potential (or potential energy) of the E-field of a point charge at different x-y points is V(x,y) = k Q/r:
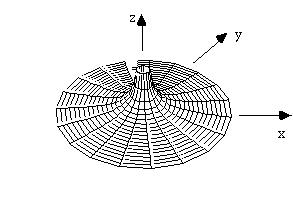
The circular contour lines are also equipotentials (Fixed V means constant radius in this case)
Partial Derivatives
(Reminder:
df/dx = lim(dx->0) [f(x+dx)-f(x)]/dx.
Think about the physical interpretation, as a slope! )
We will want to know about how functions or fields vary as you move in particular directions. If f = f(x,y), a function of x and y,
is the change of f in the x direction, with y held constant, at some fixed
point (x0,y0). (The 2nd notation is a little weird, it doesn't mean the x
component of a vector. f here is not a vector, its a scalar function!)
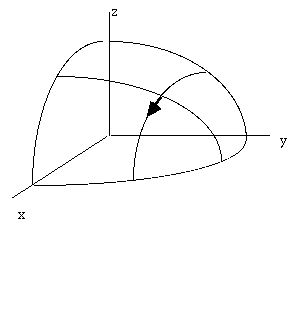
Think of plotting z = f(x,y), and the arrow here shows
Delta f / Delta x (at fixed y)
Example: f(x,y) = x2y-y2.
Partial of f (w.r.t.) x = 2 x y
Partial of f (w.r.t.) y=x2-2y
Or, our previous example, V = k Q / sqrt(x2+y2)
Partial of V (w.r.t.) y = k Q y/(x2+y2)(3/2) = (k Q/r)(y/r2)
When x gets bigger, r gets bigger, and the slope in the y direction gets less. (Look at the picture - it is generally less steep in the y direction when you are further from the origin)
Here is the Next lecture