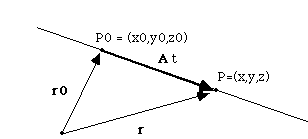
r = r0 + At.
This is called a parametric equation of a line.
In components, this equation says
x = x0 + a t
y = y0 + bt.
If you eliminate t, you get back to the same old equation for the line.
In 3-D, you do exactly the same. A line parallel to A = ai + b j + ck running through the point (x0,y0,z0) can be described as either
(x-x0)/a = (y-y0)/b = (z-z0)/c (if a,b,c are not 0), or else as
r = r0+At.
which, in components, gives
x = x0 + a t
y = y0 + b t
z = z0 + c t.
If you think of t as time, this gives you the position of a point moving along the line! (a is like the velocity in the x direction)
The velocity of a particle running along the line is dr/dt = A, a vector along the line of motion.
An example: What is the equation of a line passing through the point (1,2,3), in the direction i - k?
A: Line has equation r = r0+A t, or
(x, y, z) = (1, 2, 3) + (1, 0, -1) t, so
x=1+t
y=2
z=3-t
Writing this "symmetrically" gives
(x-1) = (3-z), and y=2
Another example: What is the equation of the line passing through the points (1,2,3) and (3,2,1)?
A: Draw a picture just like the one above, letting P0 be (1,2,3), and P be (3,2,1). Then, I can write the vector connecting them as
dr = (3-1,2-2,1-3) = (2,0,-2).
Solution 1:
r = r0 + dr t', i.e.
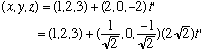I can even define t = 2 sqrt(2) t', so
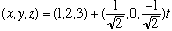
Solution 2:
Any point (x,y,z) on the line must satisfy (x-1)/(3-1) =(z-3)/(1-3), and y=2
But, this is precisely the same statement, at least, if I divide by 2 sqrt(2), and look at the components of solution 1, with t' eliminated.
How about equations for planes?
We define a plane by giving a point in it (x0, y0, z0), and a vector N = (a,b,c) which is normal to it.
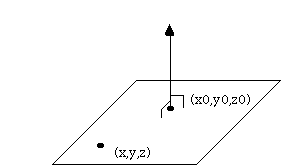
So, any vector
r = (x-x0,y-y0,z-z0) in the plane will have to be perpendicular to N, i.e.
r.N = 0, i.e.
(x-x0)a+ (y-y0)b+ (z-z0)c = 0
This is the equation for our plane!
(Equivalently, a x + b y + c z = a x0 + b y0 + c z0 = d)
Example: Find the plane containing the points
A=(1, 2, 3), B = (1, 0, -1), C= (0, 2, 4)
A: Pick any two pairs, and cross their differences. Since the differences lie in the plane, their cross product will give us N. So, e.g.
AB = (1-1, 0-2, -1-3) = (0, -2, -4)
AC = (0-1, 2-2, 4-3) = (-1, 0, 1)
Now, we can pick any of the 3 points to get our equation, so e.g.
picking A:
(-2)(x-1) + 4(y-2) -2(z-3) = 0, or
-2x + 4y - 2z = 0
Picking B:
(-2)(x-1) + 4(y-0) - 2(z+1) = 0, or
-2x + 4y - 2z = 0 (same, of course! A useful check...)
Distance from a point to a plane:
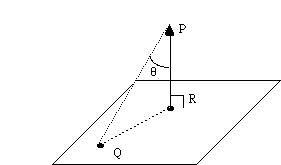
We want |PR|. PR is normal to the plane. Q is an arbitrary point in the plane. Note that
|PR|=|PQ| cos(theta)
= |PQ.n| (where n is the unit normal to the plane) So, we only need any old arbitrary point Q in the plane, and the unit normal, to get |PR|.
Example: What is the distance from the point P=(2, 2, 0) to the plane in the previous example?
A: In the previous example, the plane was -2x + 4y - 2z = 0, from which we can find the normal, N = (-2, 4, -2) (just read off the coefficients!)
So the unit norm is
.
(Now, pick any old point, e.g. Q = B = (1, 0,- 1) lying in the plane.
So, the vector PQ = (2, 2, 0) - (1, 0, -1) = (1,2,1), and then
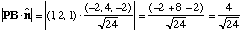
Distance of a point to a line.
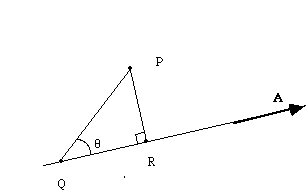
Again, Q is arbitrary, and PR is perpendicular to the line, so
|PR| = distance = |PQ|sin(theta)
= |PQ x a|, where a is the unit vector in the direction of A.
So, since the equation of a line (either form) gives you A, you just normalize to get a = A/|A|, and then take the cross product.
Here is the Next lecture