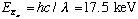.
Bohr's formula predicts
Ex: Mo (Z=42) has a K_alpha wavelength of 0.71A.
So
.
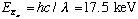Bohr's formula predicts
Not bad agreement.
NB: Z(Cr)=24 -> much lower energy (longer wavelength)
Z(W)=74 => much higher energy (shorter wavelength)
So neither one appears on the same scale as the X-ray curve I showed earlier, that's why those curves didn't show any clear bumps.
X-rays won't ever be produced if our electrons don't have enough energy to knock out the deep K-shell electron in the first place. This idea leads to the following picture of X ray absorption coefficient versus frequency:
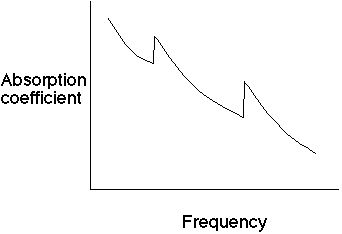
The first jump (the first "edge" in the plot) is called the "L absorption edge", and the next one is the "K absorption edge". This is a way to measure the ionization energy of each shell.
If the frequency (incoming energy) is just below the required energy to lift out a K electron, it doesn't have a very good chance of getting absorbed. But if it has just the right energy, it will knock out the K shell electron and get strongly absorbed. (F+T 1-11 is a fun historical section on the development of X-ray detection/spectroscopes. Read it on your own if you're interested!)
Conclusions so far: Bohr's picture, on top of Rutherford's, was powerful and important. It was also very ad hoc - it didn't explain why electrons don't radiate when in stationary orbits. It worked great (c.f. all these examples!) but not perfectly. E.g., Bohr could not predict plain old He spectrum (2 electrons). Let us see a hint of what must come next....
In the Bohr atom, we've seen
,
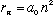and also
.
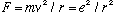So, angular momentum L = r p = mvr of an electron is given by
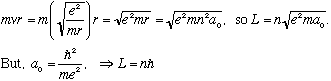
Angular momentum is quantized! Actually, the L of hydrogen levels turns out to start at L=0. This is a failure of Bohr's model. We will fix this failure when we have a correct quantum mechanical model of Hydrogen. Remember, Bohr's model is just a crude stepping stone, and not the final theory!
Many textbooks even begin with the statement that
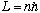as a starting postulate to derive the Bohr model, without ever appealing to the
Rydberg result, or our "correspondence" arguments, i.e. by assuming
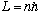you can derive the hydrogen spectrum from scratch.
One final feature to notice. Recall for photons, momentum
.
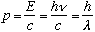Imagine you wanted to fit a photon on a circle.
You would need an integer number of wavelengths running around the circle. otherwise the wave doesn't "fit" around the circle. Mathematically:
.
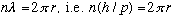By combining the classical equations for the orbit with Bohr's results, we just showed that L is quantized, that is
This means that in the Bohr model, electrons automatically satisfy
precisely the condition for a wave to fit evenly on a circle this size. What
could this be telling us? Is an electron somehow a wave, with
,
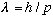just like a photon?..
(This can also be taken as a starting postulate, from which again the whole Bohr model is derived. It's really all equivalent)
Recall for photons, we have shown earlier that:
.
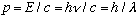De Broglie hypothesized that this final relation (p=h/lambda) should continue
to hold for massive particles as well - that they have an "associated"
wavelength,
.
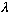The first step in the above relation isn't right for massive particles, though, so we need to review some relativity here. For non relativistic particles, momentum is p=mv. This is still true for relativistic particles, if we allow the m in this equation to be the relativistic mass (NOT the rest mass!) Earlier, we wrote down two key relativity equations:
(In both cases, E is the total energy) The first relation connects energy, momentum, and rest mass m_0. The second connects energy and relativistic mass m. If you replace p with mv in the RHS of the first equation, and E with mc^2 in the LHS, you get an equation connecting m with v, namely
.
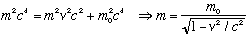This means that for relativistic particles, we can also write
.
Here is the Next lecture
Back to the list of lectures