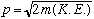. Last time we finished by reviewing a bit of relativity. We continue by introducing the notion of kinetic energy. For non relativistic particles, kinetic energy (K.E.) can be written as either (1/2) mv^2, or p^2/(2m) (same thing). Solve for momentum:
.
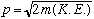This is the non relativistic connection of p, m and K.E.
For relativistic particles, this formula will look a little different. The
total energy of a relativistic particle is mc^2. The rest energy is
.
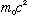The kinetic energy (energy of motion) should be the difference between total energy and rest energy. I.e.,
.
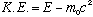Combining this with our connection between total energy, momentum, and rest mass, we get
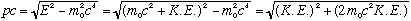
Solving for momentum, this gives us our relativistic extension of the
connection of p, m, and K.E:
.
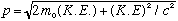Note that if K.E. is small, the second term is tiny, and this equation smoothly reduces to the usual non-relativistic formula, as it must!
For huge K.E, on the other hand, the first term is the tiny one, and this formula becomes p = K.E./c -> E/c, which is the "ultra relativistic limit", e.g. for photons.
De Broglie arrived at his prediction by considering the possibility that
photons might have a small rest mass - just too small to have been
experimentally observed yet. He then took the formulas we developed for
photons, and generalized to the case that m is not so small at all.
Experimentally, he seems to have been quite wrong about this idea - if the
photon has a mass, it is incredibly small from modern experimental data,
and current theoretical ideas insist that it be truly massless. Nevertheless,
his final conclusion,
,
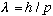still appears to be quite correct.
Some examples:
1) Consider me. My mass is about 50 kg, and if I go jogging, say 0.5 m/s (this is about 7 mph), then my "de Broglie wavelength" is
.
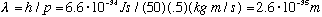If you recall that a nucleus has a size of about 10^(-15) meter, you'll realize that my wavelength is immeasurably, absurdly small.
On the other hand
2) Consider an electron, traveling with a typical atomic velocity of say 5 million m/s. Then
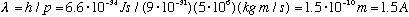
The wavelength is about the same size as the atom itself => this will be important!
What exactly are these waves, though? Waves of what? The modern picture
is that there is a wave function,
,
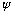a purely mathematical entity which travels along, obeying a wave equation,
associated with the particle. In fact, later we will interpret the probability
of finding a particle at a given spot (x) as being given by
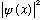(positive definite, good!) The amplitude, or wave function,
,
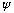really has no direct physical significance. But
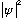tells you whether you're likely to find the particle at some given place (and
time). Large value of
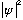means the particle is probably there. Small value means it is probably not
there. The probability is of course different from the thing. A 20% chance of
rain doesn't mean a light rain. There is no such thing as 20% of an electron.
But it is certainly possible that there is only a 20% chance of finding
an electron at a given time and place. We will talk a lot more about this wave
function soon, but it's important that you not think of e.g. an electron
as "waving" with a de Broglie wavelength....
Mathematical digression:
Here we need to go back and do a review of waves, and then we can ask some simple questions about de Broglie waves. (like, how fast do they travel? Think about that a bit...)
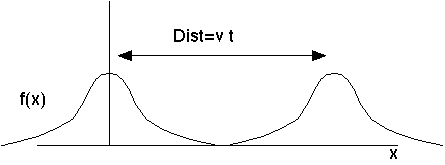
Here's a wave moving to the right. If the wave shape at time zero has the form y=f(x), then a (non-dispersive) moving wave will have a shape at later time y=f(x-Vt).
It's the same f, so it's the same shape, just located at a shifted value of x. Left moving waves will have the shape y=f(x+Vt). Any point on the wave travels at (x-Vt=constant), i.e. with velocity V. This is called the "phase velocity", because if you think of f as a sin wave, then this is the velocity that any given phase (like e.g., Pi/2, the peak) moves.
This wave satisfies a wave equation, namely
.
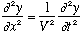Why? We have
.
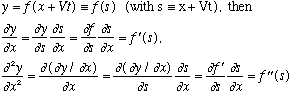Also,
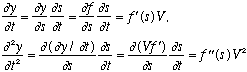
Putting these together gives the (1-D) wave equation. Notice that if you replace V with -V, the equation is unchanged. In other words, it yields both left and right moving waves as solutions. Any function f can solve this wave equation, but the simplest form of a wave is the "harmonic wave", i.e. sinusoidal:
.
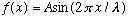The traveling wave is then
.
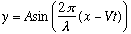(A is the amplitude.)
Notice that if you replace x with x+(n
)
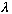(where n is any integer) then y is unchanged (so,
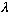is the "period" in space, i.e. the wavelength). Similarly, if you replace t
with t+(n
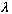/V),
then y is again unchanged. So, T=
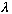/V
is the period (in time). Thus, we find the frequency
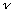=1/T
=V/
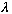= # oscillations/sec, and the angular frequency
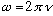= # radians/sec. Combining, we get
V=
,
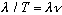which is the usual velocity equation we've been using all along (with V=c) for
light.
We can define the wave number,
k=
,
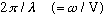which tells you the number of radians/meter, and then
.
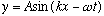Of course, if y(x=0,t=0) is not zero, you can always add any phase you like,
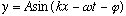still solves the same wave equation.
We can also use cosine instead of sin (this is the SAME function, just phase shifted).
In fact, we could make use of Euler's theorem (
)
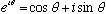to use a pseudo-fictitious function,
,
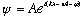and then the real waves would be represented by the real (or imaginary) part of this function. Complex forms are often much easier to manipulate, and at the end of the day you can always just take the Real part. So, our wave equation would be written as
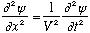
The real part of this equation is itself the same wave equation, so if
the complex function
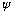satisfies this complex differential equation, the real part of
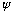satisfies the equivalent real wave equation.
Note that if
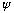works, the complex conjugate
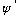also works.
Also, this equation is linear. If
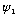works and
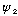works, then
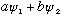does too. I.e., wave solutions can be superposed.
Consider two equal amplitude waves (but not necessarily in phase), and add them up
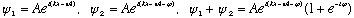
The sum has the same velocity (V=
),
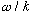wavelength, and frequency, but the amplitude is not the same. Let's find
the resultant amplitude:
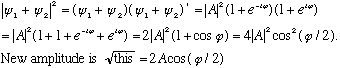
The new amplitude can be anything from 0 to 2A, this is interference!
Here is the Next lecture
Back to the list of lectures