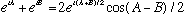.(continued)
Now consider adding two waves with nearly the same k and frequency, but not quite. Use the mathematical identity
.
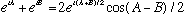Proof: use
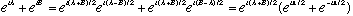
Which gives
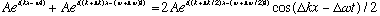
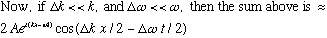
What's the picture? We're adding 2 nearly identical waves, and get back just
what we started with, times
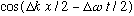(which is a "modulation" of the amplitude)
The carrier wave is
,
which moves at velocity V =
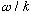
(also called the phase velocity above). But the modulation is itself also waving, and it moves with a velocity (called the "group velocity") given by
For light in a vacuum, c is a constant,
,
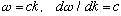there's no difference! Phase velocity and group velocity is the same! But matter waves will be different:
.
This means that the velocity of a matter wave is not constant, it varies with the wavelength (this is quite different from light!), and the phase and group velocities will differ.
(Quiz today...)
Here is the Next lecture
Back to the list of lectures