and also
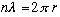(i.e. "fitting an electron wave on a circle") gave us the Bohr model!
Ultimately, to get to a "compleat theory", we will need to find the
appropriate wave equation satisfied by our matter waves. But even before
we do that, our crude and qualitative picture we're developing yields some nice
results. E.g., we saw that saying
and also
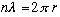(i.e. "fitting an electron wave on a circle") gave us the Bohr model!
Here's another: Suppose we put a particle in a box
(The first is an ordinary box, the second might be like a pool table, the third e.g. a bead on a frictionless wire)
We want the wave function
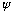we've talked about - the thing whose square represents the probability of
finding the particle at some position. For a box, we expect that
should be zero (0) outside the box.
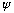should be zero (0) at the walls.
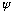should be some kind of wave, or a sum of waves, because to represent a particle
it should ultimately be related to de Broglie's waves..
If
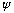is a sine wave, then we really need for it to fit in the box. That is:
(etc.)
This means that
,
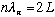which in turn means
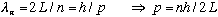
The kinetic energy will be
.
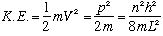So, not just any old energy is allowed! You may only have
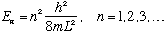
n is called the quantum number, and E_n is the energy level.
Confining the particle restricts the energy. (You can't have a pool ball with arbitrary energy according to this picture!) Of course, this happened when we confined an electron in hydrogen too.
Also, zero energy is not a solution, because the corresponding sin wave would be flat, i.e. no particle. So there is a minimum allowed energy, given when n=1.
h (Planck's constant) is very small, so on a pool table, you simply never notice that the balls are not allowed to have continuous energies. You might be puzzled by the idea that you cannot stop a pool ball either, but let's compute the minimum allowed speed:
For an ordinary table, this gives v_1 =
.
It would take this ball about 10^15 times the age of the universe to make it across the table. (Could you ever detect the difference between this speed and zero?)
Next example: Try to put an electron in a box 0.1 nm (= 1 Angstrom) across. This is the size of an atom! Now,
The scale of energy, a couple dozen eV, is coming out correctly. Clearly, hydrogen is not exactly a box, since the Bohr spectrum is rather different. (It doesn't have sharp walls, that's the main difference)
This particle cannot be ionized, since the energy goes to +infinity at large n. (But that makes sense, it's trapped in a box!)
We will return to the box problem soon, armed with more power. But first, one more discussion based on de Broglie's idea...
If particles are to be associated with a traveling wave group, and the wave represents the probability amplitude, then we cannot measure exactly the momentum and position simultaneously! Why not?
,
so if you want to know the momentum, you must definitely know the wavelength.
But, the only wave with a definite wavelength is one that runs forever! (And a
long wave means the particle could be anywhere) Any other wave is a wave
packet, that will be built up by a (Fourier) sum of different momenta, i.e.
different wavelengths.
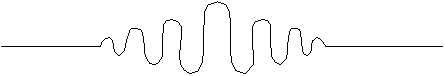
A short packet like this has a much better defined position, but must be built out of various different wavelengths. To do this formally, we would need to use Fourier transforms. We'll save the mathematical details for Jr. level quantum. But, the rough idea is as follows:
You need a range of wavelengths, added together, to built a localized packet.
The Fourier transform (F.T.)of
tells you precisely what amplitudes you need for each wavelength, so the F.T.
tells you what range of wavelengths will be needed. Strictly speaking, you need
ALL wavelength, but usually they are concentrated in a small region of
wavelengths. For ease of picturing, think of the real F.T., given by
,
here g(k) is the F.T. of our wave function, and k is the wave number. Here are
some example of wave functions and their approximate F.T.'s:
We learned in 2140 that the width (
)
of a pulse tells you (roughly) the width
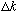of the Fourier transform. In fact,
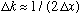(Exactly equal for Gaussians), which means that
This final result is also known as the Heisenberg uncertainty principle, it relates the uncertainty (or spread) in momenta associated with a particle to the uncertainty in position.
Bottom line: For any wave packet, we have
,
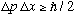the Heisenberg uncertainty principle.
Why the >= sign? Because, for Gaussian wave packets it's strictly an equal sign, but Fourier transform theory says that any other wave shape only makes the resulting width (ambiguity) in p larger.
This relation is not about our poor instruments. It's not about poor statistics. It's apparently a basic rule of nature. The more well defined a particle's position, the less well defined the momentum (i.e., you need more wavelengths to build up a narrow wave packet. Or, put another way, you must superpose many different wavelength waves to construct the desired wave function) And vice versa, the better well defined momentum is, the more your "packet" looks like a pure sin wave, which means it gets very long, and you no longer have any good information about where the particle is. (Please also bear in mind just how small Planck's constant is - this uncertainty principle is generally effectively completely irrelevant for ordinary sized objects.)
Here is the Next lecture
Back to the list of lectures