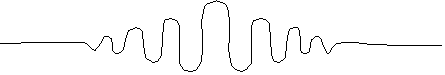
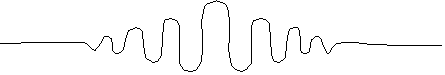
Say it's
wide. The square of this wave function tells you where the particle is
likely to be, which means basically it could be anywhere in that packet
(although it's admittedly slightly more likely to be towards the middle, where
it's biggest) So, the uncertainty in the position of the associated particle is
roughly
.
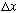Now, how many wavelengths are there in the pulse? Count them! Say it's
N. But, for finite wave trains, it's always hard to count those last tiny
little wiggles! Maybe its N +/-1, for safety sake. So this means
.
Note also that the wavelength sometimes varies a little bit over the wave
packet. We'll just use the average wavelength,
,
and lump the wavelength variation effects in with the +/-1 too) So what
momentum does this packet have? De Broglie says
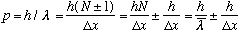
Which means there's some uncertainty in the momentum, due to our uncertainty in counting wavelengths. And once again, we see that the uncertainty in p (the +/- part) is given by
.
Please bear in mind that this argument is very sloppy. Fourier transforms really tell you the answer precisely, no matter what the wave packets look like. (This argument makes it seem like the problem is with our eyes, trying to count, but it's much deeper. The exact number of wavelengths in a finite packet is really and truly ill defined!)
Bottom line, once again: For any wave packet, we have
,
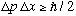the Heisenberg uncertainty principle.
Let's see some examples:
A (free) proton is located somewhere, with an uncertainty in position of
m.
What is the uncertainty in its position 1 second later?
Since
.
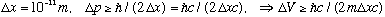We just can't know its velocity better than this. So, after one second, we
don't know its displacement to better than
This uncertainty principle is sometimes derived in a more "physical way". E.g.,
suppose you wish to locate a particle, mass m, using a microscope. If you shine
light on it, with wavelength
,
you will locate it to within
.
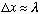(No better!) At the same time, the photon carries some momentum,
.
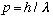It bounces off the particle, but which way? The recoiling electron may go off,
carrying a momentum change of
once again. I don't personally like this argument as well, though, because it
seems to imply that the uncertainty is just the "fault" of the interaction.
(and thus perhaps, one could get clever and someday, somehow work around it?)
The Fourier transform arguments above say that in reality, the wave nature of
particles make this uncertainty principle truly intrinsic to the nature
of particles.
Another example. Hydrogen atoms are about 0.5 A big. What sort of energy do we expect the electron to have, inside an H atom?
.
Now, the electrons run around in circles, so if the above gives the uncertainty in p, it means one expects that the typical momentum should also be 2000 eV/c) (Sometimes towards, sometimes away, sometimes left, ....
The uncertainty is roughly the same as the typical momentum, itself. At least, within factors of 2 or so)
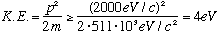
Recalling that
,
this means that the correct answer should be K.E. =+13.6 eV
We're off by a factor of 3, not bad for such a crude and simple estimate! (and,
p = 2
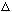p
seems more reasonable from the picture, anyway, which would have given 16 eV)
Finally, note that by my same heuristic argument from above, a wave group in time will have N +/-1 periods, T, so the total time the group is present will be
More formal (Fourier transform) arguments give
,
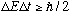another form of the Heisenberg uncertainty principle.
Here is the Next lecture
Back to the list of lectures