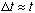 (that is, such atoms can live as long as 2 ns, or as little as a fraction of a
ns)
(that is, such atoms can live as long as 2 ns, or as little as a fraction of a
ns)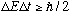 ,
another form of the Heisenberg uncertainty principle.
,
another form of the Heisenberg uncertainty principle.
So, e.g., if an excited atom lives on average about 1 nanosec (ns), there will
be some uncertainty in its lifetime too. Typically, this uncertainty is of the
same order as the time itself,
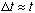 (that is, such atoms can live as long as 2 ns, or as little as a fraction of a
ns)
(that is, such atoms can live as long as 2 ns, or as little as a fraction of a
ns)
This gives us the following estimate of the uncertainty in the energy:
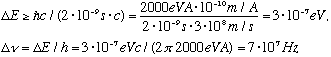
This means the light coming from these atoms, as the electron decays, will not be a sharp line, but will have a spread of frequencies! Recall for hydrogen, frequency is about 10^15 Hz or so, so this width is very tiny, but it is measurable. (In reality, there are yet other effects which can broaden the hydrogen lines even more than this)
Another uncertainty principle example:
Radioactive decay in nuclei often releases electrons, with energies that typically range up to an MeV or so. You might be tempted to ask if that electron comes from inside the nucleus (i.e. trapped in the electromagnetic "box" made by the protons). We can use the uncertainty principle to see how much energy that electron would have while trapped, knowing only that nuclei are about 5 fm in size.
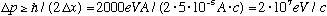 .
.
This implies an energy given by
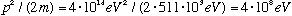
Uh oh! This is >> 511 keV, so must use relativity!!
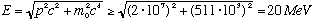 .
.
This is ten times larger than the observed energies, which implies that is very unlikely that the electron is present, stuck inside the nucleus, waiting to be freed. If it was there, it would have too much energy! (The electron is in reality created during the process of radioactive decay, in a certain sense outside the nucleus)
This just about concludes how far we can go, armed only with de Broglies "simple" idea. (See Bloch's quote, F+T p. 105) We have seen that in the world of very small scales, we will no longer be able to use Newton's laws, like F=ma=m(d^2x/dt^2), because x itself is ill-defined (or uncertain, however you want to put it). In the end, we are going to describe a new mechanics, Quantum Mechanics, and it will deal only with probabilities! This may seem frustrating, (like classical mechanics was somehow better), but classical mechanics is a direct consequence of quantum! That's because ordinary objects are made up of so many (quantum) atoms, that departures from average behaviour aren't noticeable. So, e.g., Bohr's model statement that the electron in hydrogen's ground state is 0.53 A away from the proton will turn out to be quite incorrect. Any given measurement could result in larger or smaller values. But the average value will turn out to be 0.53 A!
The quantity we will work with from now on, which we've talked a bit about
already, is the wave function,
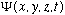 .
(psi)
.
(psi)
It will be complex, so we can write

The latter is real, and positive definite. If
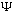 is truly a probability amplitude, then
is truly a probability amplitude, then
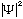 is proportional to the probability of finding a particle at the point
(x,y,z,t)
is proportional to the probability of finding a particle at the point
(x,y,z,t)
The particle must be somewhere, so we usually choose to "normalize the wave function", that is we require that
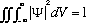
If you calculate
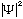 in some problem, you may (sometimes) get a different answer for this integral,
which just means you did not properly normalize your wave function. This is
easy to fix (we'll see how soon). With this normalization, we also see what the
proportionality constant is, it's the volume! That is, the probability that the
particle is in any given finite volume V is
in some problem, you may (sometimes) get a different answer for this integral,
which just means you did not properly normalize your wave function. This is
easy to fix (we'll see how soon). With this normalization, we also see what the
proportionality constant is, it's the volume! That is, the probability that the
particle is in any given finite volume V is
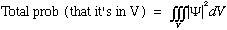
which means we should really interpret
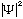 technically as the probability per unit volume. In one dimension, the
probability to find the particle between x1 and x2 is just
technically as the probability per unit volume. In one dimension, the
probability to find the particle between x1 and x2 is just
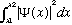 .
.
This means, for small regions, that the
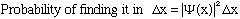
I have argued that free particles, with a well defined wavelength (and thus momentum) should just be represented by the usual old traveling wave formula, so a simple free particle ("free wave", "plane wave") has a wave function of
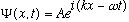
I really do not prove this (!), I simply postulate it. It's pretty much just de Broglie's idea, restated in Schrodinger's way, and we've already used it and assumed it in talking about de Broglie waves.
For a physical (string-like, or EM) wave, I would probably take either the Real
or Imaginary part of this, and just discard the other. But since I like
the idea that this wave function should represent an infinitely long wave
train, i.e. a particle equally likely to be found anywhere, I leave it as fully
complex. Why? Because probability is proportional to
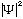 =|A|^2=constant,
i.e. a uniform probability. (Sin's and cos's have zeros, which seems a
bit unpleasant. This complex form is indeed essential.)
=|A|^2=constant,
i.e. a uniform probability. (Sin's and cos's have zeros, which seems a
bit unpleasant. This complex form is indeed essential.)
Here is the Next lecture
Back to the list of lectures