

We can combine these to form some very useful identities, which are worth remembering.
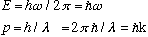 .
.
So, I can rewrite my free-particle wave function as
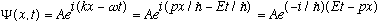 .
.
This expresses our wave function in terms of more "familiar" parameters, energy and momentum (rather than frequency and wave number). Now, presumably, this wave function should really arise because of some underlying differential equation. We shouldn't have to just postulate it out of thin air, it should solve some fundamental wave equation which describes matter waves. For ordinary old waves (like light), we had such an equation:
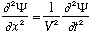 .
.
Indeed, the wave function I wrote down above does satisfy this equation,
with V=
 =E/p.
But there's already something wrong for non-relativistic particles (which we're
going to be mostly interested in this semester!), because E/p is not equal to V
for low V's!!
=E/p.
But there's already something wrong for non-relativistic particles (which we're
going to be mostly interested in this semester!), because E/p is not equal to V
for low V's!!
(E/p -> (1/2)mv^2/(mv) = v/2)
We must hunt for a new wave equation which works properly for non-relativistic particles. Erwin Schrodinger, in 1925, found this wave equation. I must emphasize to you that this underlying equation is not going to be derived! We cannot derive it from Newton's law, or anything like that. It's a new law of physics. We're going to have to guess it. We'll try to make it as plausible as possible, consistent with all the ideas discussed so far. In the end, though, it will be a postulate, and we have to do experiments (and calculations) to see if it works. (And it does, of course, brilliantly!)
"Schrodinger's equation cannot be derived from first principles. It is a first principle".
Where are we headed? Classical mechanics is based on the relation

Converting to our quantum partners,
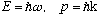 would give
would give
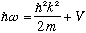 .
.
(This is all non-relativistic for now, let's keep life simple if we can!)
Now look at my proposed free particle wave function ("free" means no potential, V=0)
 .
.
So notice that
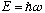 is just going to fall out if I take one derivative with respect to t,
i.e.
is just going to fall out if I take one derivative with respect to t,
i.e.
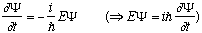
Also notice that
 will just fall out if I take two derivatives with respect to x, i.e.
will just fall out if I take two derivatives with respect to x, i.e.
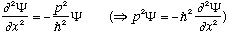 .
.
So if I want to have
 ,
then I would surely also want
,
then I would surely also want
 ,
and this means, from the above,
,
and this means, from the above,
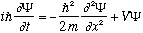
In 3-dimensions, a traveling wave is just
 ,
and we would get
,
and we would get

(the 3 terms in parentheses represent
 )
)
This is also called Schrodinger's time dependent 3-D wave equation:

Notice that I "derived" this from the V=0 solution, so the V term just got added in, in a (hopefully) plausible way. It will turn out to be completely successful for an incredibly wide variety of problems. However, relativistic particles will require a new equation. (Dirac came up with this, ultimately). By the way, Newton's second law of motion (F=ma) will turn out to be a consequence of the Schrodinger equation.
We can write down Schrodingers (1-D) equation in several ways, each of which will turn out to be useful:

For "stationary state" problems, (like e.g. what are the allowed energy levels in an atom?), the second form is easier to deal with.
An important property of the S.E. is that we have a partial differential
equation which
 satisfies. The equation is linear, so if
satisfies. The equation is linear, so if
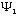 and
and
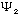 are solutions, then
are solutions, then
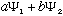 is too! This means our wave functions obey the principle of superposition, a
basic and essential property of waves. So, e.g. we expect to get out
2-slit interference, which we will want.
is too! This means our wave functions obey the principle of superposition, a
basic and essential property of waves. So, e.g. we expect to get out
2-slit interference, which we will want.
The function
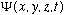 is going to contain all the information that exists about our particle,
even if it is only in the form of probabilities. It will tell us more than just
the position information: it contains buried in it information on energy,
momentum, angular momentum, and more. Perhaps you can see that directly from
the S.E.:
is going to contain all the information that exists about our particle,
even if it is only in the form of probabilities. It will tell us more than just
the position information: it contains buried in it information on energy,
momentum, angular momentum, and more. Perhaps you can see that directly from
the S.E.:
 .
If I were to give you
.
If I were to give you
 ,
then you can calculate E by using the left side of this equation. (Or simpler
still, from the equation
,
then you can calculate E by using the left side of this equation. (Or simpler
still, from the equation
 .
Similarly, from the equation
.
Similarly, from the equation
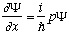 you can calculate p, etc.
you can calculate p, etc.
Some of these quantities are quantized (like the energy), and some are not (like the position, or sometimes momentum, which have a spread of values) For those which are spread out, we might be interested in an "average" value, or an "expectation value", which we write as
<x> = Expectation value of the position of a particle which is described
by
 .
.
(for this quantity, you probably don't want to think of the free wave, which is infinitely long, and really has a very ill-defined <x>. Think instead of a particle in a box, or in hydrogen's ground state, or simply a "wave packet" which is a superposition of free waves that is localized in space)
Sidetrack: Expectation values
If the probability of measuring a particular value, x, is P(x), then

Why is this? Think of the problem of averaging test scores, given like this: {s} = 5,1,3,8,4,5,6,8
The simplest way is
<s>= (S1+S2+S3+...+SN)/N=(5+1+3+8+4+5+6+8)/8=5.0
But I could think of it in a slightly different way. Group things by the number of scores for each possible value
< s > =
[1*(1 time) +
2*(0 times) +
3*(1 time) +
4*(1 time) +
5*(2 times) +
6*(1 time) +
7*(0 times) +
8*(2 times) ] /
(1 + 0 + 1 + 1 + 2 + 1 + 0 + 2)
=40/8=5.0
It's exactly the same thing, of course, I just grouped up multiple scores with the same value.
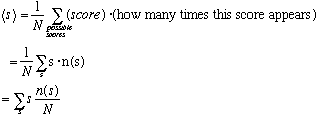
where n(s) is the number of times the score s appeared, meaning
n(s)/N has a nice interpretation, it is the fraction of the time that the score s appears. So, 1 appears 1/8 of time, 2 appears 0/8 of time, ... 5 appears 2/8 of time, etc. If these test scores were randomly distributed, I might think of the fraction of time as being the probability. i.e.
1 has probability 1/8, 2 has prob. 0/8, 5 has prob 2/8, etc.
Note that by definition,
 ,
because the n(s)'s have to add up to N. This is the same as saying that the sum
of probabilities must = 1. Thus, calling n(s)/N the probability of getting
score s, we have
,
because the n(s)'s have to add up to N. This is the same as saying that the sum
of probabilities must = 1. Thus, calling n(s)/N the probability of getting
score s, we have
 .
.
This is what I claimed above, only instead of scores s, it was position values x:
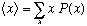
Since x can be anything at all, the sum becomes an integral, and P(x) becomes
 .
.
Bottom line:

Graphically:

Note: This argument only works if
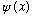 is normalized, i.e.
is normalized, i.e.
 ,
because otherwise
,
because otherwise
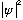 is not the probability (it's only proportional) But notice that the S.E. is
linear, so if
is not the probability (it's only proportional) But notice that the S.E. is
linear, so if
 is a solution, then so is
is a solution, then so is
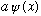 (for any a). So, if you solve the S.E., and get some
(for any a). So, if you solve the S.E., and get some
 ,
and then discover that it's not normalized, i.e.
,
and then discover that it's not normalized, i.e.
 ,
then
,
then
 is also a solution, and
is also a solution, and
 ,
which means that
,
which means that
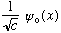 solves the S.E. and it is normalized to boot. This means you can always
normalize your solutions to the S.E., and it's usually a good idea.
solves the S.E. and it is normalized to boot. This means you can always
normalize your solutions to the S.E., and it's usually a good idea.
Once you have, you can find average values of other functions besides just x. E.g., you might measure x^2 instead of x, and average these, and the exact same probability argument would give"

N.B. <x> could be zero, or +, or -, but <x^2> will always be >=0, and will almost always be positive definite.
In general,
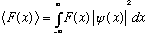 ,
which means e.g.
,
which means e.g.
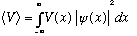 tells you the average value of the potential felt by the particle.
tells you the average value of the potential felt by the particle.
<V(x)> is not necessarily the same as V(<x>), e.g. if V=-kx^2/2.
Here's a tricky question. What is <p>? (The expectation value of the particle's momentum?) p is not a function of x, it can't be! If I tell you x, you don't know what p is (uncertainty principle says so) We can figure out <p>, and <E>, and other things which look problematic, without violating the uncertainty principle, but not just yet...
Let's go back to the S.E., and consider the case that the potential energy does
not change with time, explicitly. (I.e. forces depend only on position.)
We are interested in so-called "stationary states", like the allowed energy
levels in an atom. The free vibrations which any system allows will be much
like standing waves, or normal modes, of any vibrating system (organ pipe,
guitar string, microwave cavity, ...) That is, you expect
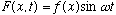 for classical strings. The shape may be complicated, but every piece of
the string vibrates at the same frequency,
for classical strings. The shape may be complicated, but every piece of
the string vibrates at the same frequency,
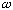 .
We say that the space and time dependences separate.
.
We say that the space and time dependences separate.
Similarly, our wave function will have this separation property too:
 .
.
One can prove that if V=V(x), then the wave function will always be separable like this.
So recall that
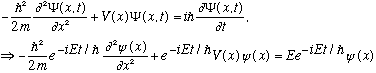
Cancel the exponential term (it can never be 0, so that's o.k!)
 .
.
We wrote this equation before, but with the full wave function
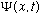 .
Now we've explicitly eliminated all mention of time, to arrive at a truly time
independent equation.
.
Now we've explicitly eliminated all mention of time, to arrive at a truly time
independent equation.
In 1-D, this is an ordinary differential equation. (The partials are total derivatives, because there's only one argument). Give me V(x), and some boundary conditions (2, because it's second order), and I'll solve this equation for you! Except, it turns out that physically/mathematically acceptable solutions (i.e. continuous, finite, single-valued, etc.) will only arise for certain special (magical) values of E, which we call "eigenvalues" of the equation. For other values of E, there simply is no stationary state. This is Schrodinger's way of explaining Bohr's quantized orbitals, if you like. Only certain values of E_n will give you an acceptable solution of this wave equation, or a "stationary state". (Those will be the Bohr energies, if the potential is a Coulomb potential....)
Here is the Next lecture
Back to the list of lectures