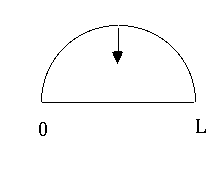
The differential equation being solved here was
,
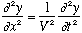the wave equation. The constraint of being zero at the edges means ONLY
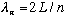are allowed,
so wavelength (and hence frequency) are quantized. You can not choose to play any tone on a string with fixed length and fixed tension (V).
We will solve the S.E. in a box shortly, and see the quantization of energy, E_n, come out in exactly the same way!
In fact, it's not just the energy that can get quantized this way. E.g., we will see in the hydrogen atom that L (angular momentum) is also quantized. Importantly, some variables will not be quantized! E.g., the distance r to the electron in hydrogen, unlike in Bohr's model, will turn out in the wave equation way of thinking, to be totally free. Any value can be measured. It will, however, have a probability distribution, and in particular:
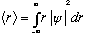will turn out to be 0.53 A for the ground state wave function.
Now that we're armed with the S.E., let's look again at the particle in a box. We will now solve the S.E., and not only will we find E_n (like we did before), we will also find the complete wave function! This means we will know essentially everything we can know about a particle in a box.
To be a valid wave function, I claim that
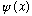must have the following properties:
It must be continuous everywhere.
It must have a continuous first derivative everywhere.
Both the function and its first derivative must be finite and single valued everywhere.
N.B.. If the first derivative were not continuous,
then the second derivative would be infinite at the point of discontinuity.
But, the S.E. says
E-V(x) is generally not infinite, and by hypothesis neither is psi, which means
from this equation that the second derivative can't be infinite either.
Thus, we would have an impossible situation if
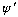were discontinuous.
We want to solve
,
where V(x) is given by:
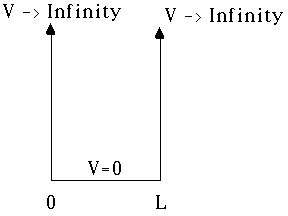
Inside 0 <=x <=L, we have V=0, and so there
Look familiar? It's our favorite diff. eq, with solution
.
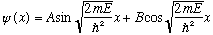Outside the region (0,L), we must have the wave function
.
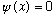(Otherwise, the S.E. would lead to impossibilities out there, with an infinite potential but finite wave function?!)
Anyway, it's physically absolutely clear that
=0
outside, because the probability is 0 outside the box!
So we need
.
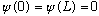(Because we require that
be continuous). This means
(n=0 is no good, because that would give
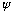=0
everywhere, which means there's no particle!
So we have (just like we got before)
,
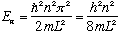and
.
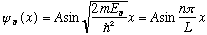This
is continuous, it's first derivative is continuous, and it is finite, and
single valued at all x. (Good!) But, is it normalized? Not yet, but A is
still undetermined. We want the total probability of finding our particle to be
1:
The last line gives the normalized wave function for a particle in a box.
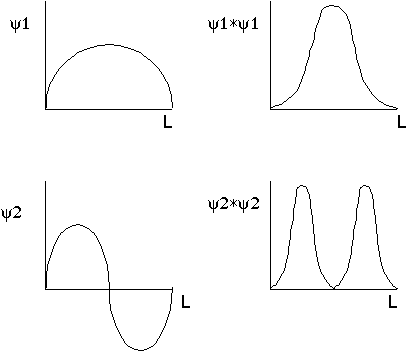
Particle is likely to be in middle for first wave function
Particle is unlikely to be in middle for second wave function.
Funky! A classical particle is equally likely to be anywhere. Not so with a quantum particle in a box. Of course, for n=big:
If your "particle locator" has width
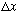(i.e. if you smear this out over anything more than a half wavelength or
so,
or average over
),
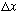then this function looks quite uniform. This is the correspondence
principle again! Large n => behaves classically.
These waves are like the oscillations of a string. The requirement that
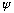be a wave, but also be 0 at the ends, has restricted what wavelengths
are possible, and what energies. The fact of quantization isn't so odd after
all - it's just what happens when you want to put a wave inside boundaries.
By the way - we found
.
Recalling that
gives the full time and space dependence (the "time evolution") if you ever wanted it.
Notice that any given solution, say the ground state, only has a definite
wavelength inside the box. If you view
as a function over all space, it does not have a unique momentum. (Think
of our F.T. arguments - you need to add up waves of various momenta to get a
packet that lives only inside a box)
In fact,
,
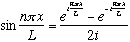so one can build
out of two waves:
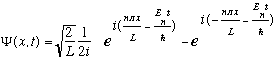
The first term represents a wave moving to the right, with wavelength 2L/n, hence momentum = nh/2L. The second term is a left moving wave, with p=-nh/2L.
This means there is a superposition of two different momenta, and there is thus an uncertainty in the momentum given by
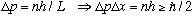
So this is a wave function with well defined energy, but the momentum is not unique. The uncertainty principle is satisfied automatically by this particle. The particle is bounded in space, which is what causes an uncertainty in the momentum. (But, if it oscillates forever, it is not bounded in time, which means it can have a definite energy)
Let's calculate the probability that the particle is, say, somewhere between x1=0.4L and x2=0.6L.
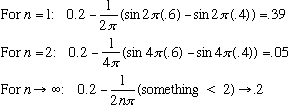
(The last is the classical result)
On the other hand, what is the expectation value of x?
I leave this integral as an exercise. Units say it must be proportional to L^2. Common sense says some fraction* L^2.
Answer is <x> = (2/L) L^2/4 = L/2, the midpoint. (Good!) True for all n, too. Even for n=2, where Prob(x=L/2)=0, it is still true that <x> = L/2.
I.e., it's just as likely to be in the left or right side.
Let's think of a different kind of (classical) system, to get more of a feel for this probability distribution. Think of a swinging pendulum, and measure its position at random times. (or, take a million pendula, and measure each one once)
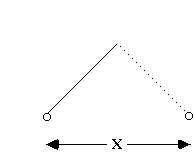
The pendulum is slow near the ends, so it spends more time there. This means that it is more likely to be found near the endpoints.
So, a plot of the "classical wave function", or in other words the probability distribution of x, is:
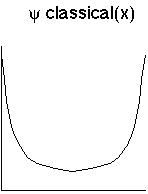
For quantum systems, we can't measure the position over and over, because measurements usually mess it up. But we can imagine many identical systems. So, this fits with the probabilistic interpretation.
Remember that for a single measurement, probability is a weird concept.
After the measurement, the answer to the question "was it in some small region,
,
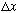is no longer
,
but yes, or no! It only makes sense when you think of an ensemble
of systems.
Here is the Next lecture
Back to the list of lectures