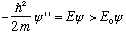 ,
which means our new wave function would be more curved.
It might look like this:
,
which means our new wave function would be more curved.
It might look like this: Next thing to notice. What would happen if E was just a bit bigger than E0, the ground state energy? Inside the box,
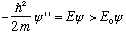 ,
which means our new wave function would be more curved.
It might look like this:
,
which means our new wave function would be more curved.
It might look like this:
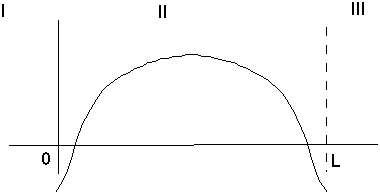
Now we have to try to match up the exponentials in regions I and III. But we discover a problem. The slope is all wrong! Exponential functions don't wiggle: if they start off going down, we'll get a solution which looks something like the following-
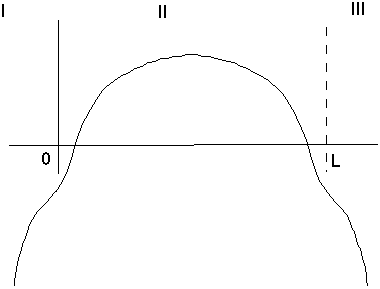
(The value and slope at the boundary are fixed, so the exponential will have to look roughly as shown.) This is no good! This means that not any old E will work. We do not get an acceptable wave function if the energy isn't something special. There's a delicate balance going on - you have to wiggle in the middle, and then be able to smoothly join up with a dying exponential at the edge.
What if we tried going to a bit lower energy, E, below E0? Then you would find:
We see that the slope is not very steep at the boundary any more. When you try
to match up a positive value, with a small slope, to an exponential of the form
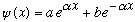 ,
your solution will look like
,
your solution will look like

You need a finite "a" term on the right, to match slope and value at the edge, and this then blows up.
Mathematically,
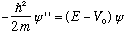 ,
but (E-V0) is negative in region III,
,
but (E-V0) is negative in region III,
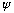 is positive, therefore
is positive, therefore
 is positive, which means the sum of exponentials must be curving up, and this
leads to a blow up.
is positive, which means the sum of exponentials must be curving up, and this
leads to a blow up.
What we can do is raise the energy quite a bit, until we get to the next stable solution, namely E2, whose corresponding wave function will look like:
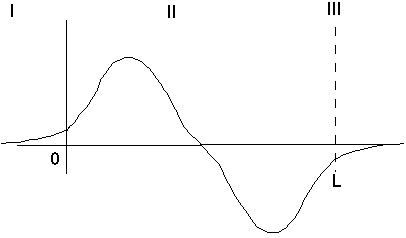
Once again, it's very delicate! If E is a bit lower than E2, then we get
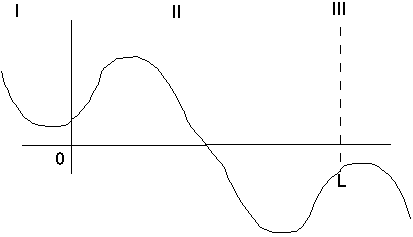
whereas if E was a bit higher than E2, we'd get something like
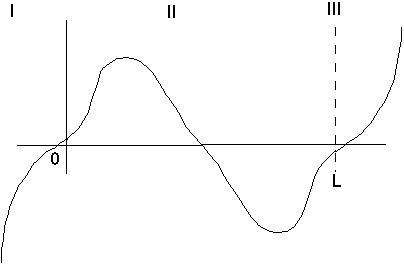
Notice also, once again, our E2 has a slightly larger wavelength than the corresponding infinite box E2, which must run down all the way to 0 at the edge.
So, E2(finite box) < E2(infinite box)
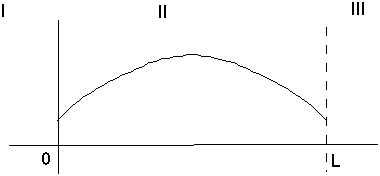
Also note, we now have a node. The next energy level, E3, will have 2 nodes, and so on. My first picture of a finite box wave function corresponds to the fifth energy level, or fifth eigenfunction.
Some more points:
If E>V, then
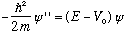 ,
so
,
so
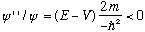
If
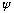 is positive,
is positive,
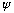 ''
is negative (curving down).
''
is negative (curving down).
If
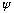 is negative,
is negative,
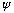 ''
is positive (curving up), i.e. it's always curving towards the axis. (like a
sin wave!)
''
is positive (curving up), i.e. it's always curving towards the axis. (like a
sin wave!)
When E<V (outside the well), the same argument shows that you always curve away from the axis. In general you do something like

If you've tuned things just right, then you can get something like
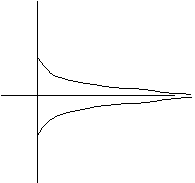
For my ground state, I drew a wave function earlier which was everywhere
positive, and had no node. But what about plotting the negative of that
function? (Just flip it around the x axis, otherwise keep it exactly the same)
This is exactly the same thing. I.e., it turns out there
is an ambiguity! If
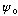 is the ground state, then not only is -
is the ground state, then not only is -
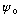 ,
but more generally
,
but more generally
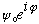 .
(for any constant value of phase,
.
(for any constant value of phase,
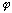 ,
whatsoever) And, all of these choices have exactly the same normalization,
because
,
whatsoever) And, all of these choices have exactly the same normalization,
because
 is identical. So, for 1-D bound states, we can choose the phase. In this
case, you can choose to make the wave function real (a h.w. problem) For
unbound states, or in general in more than 1-D, we're stuck, and the wave
function may have to be truly complex.
is identical. So, for 1-D bound states, we can choose the phase. In this
case, you can choose to make the wave function real (a h.w. problem) For
unbound states, or in general in more than 1-D, we're stuck, and the wave
function may have to be truly complex.
By the way, this "ambiguity", or freedom of choice of phase of the wave function, turns out to have very deep implications when we study relativistic quantum theories. It will turn out to be connected to gauge freedom in E+M!!
Here is the Next lecture
Back to the list of lectures