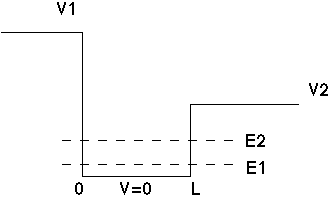
My solutions for the corresponding wave functions look something like the following:
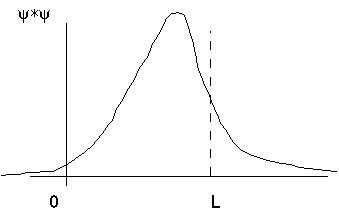
Features: In the first wave function, the exponential decay is quicker on the left side than on the right, and thus the intersection with the y axis is also lower on the left. The whole curve is somewhat right of center to allow for this. In the second wave function, the energy E2>E1, and the decay is a bit less rapid on the left side, and the intersection point is a bit higher. The node is somewhat right of center. The intersection point on the right is higher (in magnitude) than it is on the left, and also bigger (in magnitude) than the corresponding point for the first wave function. And of course, the decay on the right side of the second wave function is the least steep of all.
The total area under both of the probability curves should be one, if the wave functions are properly normalized. Inside, the potential is constant, so those curves are pure simple sine waves. Outside, they are pure simple dying exponentials. The curves are continuous, and have continuous first derivative, everywhere.
What we've been considering here is even somewhat practical. E.g., the
potential inside a metal is typically a constant,
(the work function) lower than outside. So, for a thin metal film, electrons
are "trapped" in a potential that looks just like the square well we've been
studying:
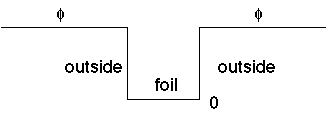
and the lopsided example might arise when a foil made of different material (and hence different work function) is placed against a metal:
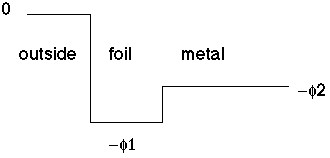
Many potentials, however, are not this sharp. The most generic potential might look like this:
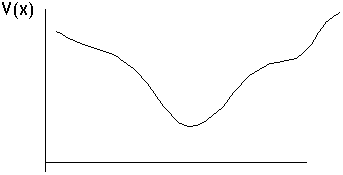
In this case, if a particle is put into this potential, with total energy E, then we can draw the following diagram:
This is more complicated. We don't have simple sine's inside, because the wavelength is different everywhere! Why? Because
KE=E-V,
which means
also varies with position, and this means p itself is varying with position,
and so the wavelength also varies. But still, our generic ideas developed above
still hold. Inside,
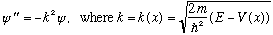
So the wave function is still always curving towards the x-axis (the concave side always points towards the x axis).
Outside,
So here, it always curves away from the x axis. (the concave side points away from the x axis).
The bigger V-E is, the sharper ("wigglier") the relative curvature. The same
ideas as before will hold - only special values of E will allow us to "hook up"
and
smoothly at the turning point, without letting
run off to infinity anywhere. Also, once again, the number of nodes will be one
less than the number of the level.
A new and interesting feature for varying depths is the effect on the maximum
value of
.
Classically, when you're someplace where E>>V, you're moving fast, and
don't spend much time there. So, you have a low probability of being found at
such places, which means a smaller
.
If E>V, but just barely, then you're moving slowly, hanging out a long time
there, and so you might expect a large
there. This classical argument doesn't always work exactly, but it does
give the right idea. Remember, we're looking at time independent solutions
("steady state", or "stationary state"), so nothing is really moving at
all! Here's the quantum version of that argument, with a varying potential that
has been simplified to consist of two flat regions next to each other. (In the
end, any smooth potential can be mocked up by a bunch of tiny steps,
flat in between)
In region I, the KE is larger, so the momentum is too, which means the wavelength is shorter there (It wiggles faster)
In region II, the KE is smaller, so the wavelength is longer there. (and should be constant throughout that region, although I didn't sketch it so beautifully...)
To match up at the middle, it turns out the amplitude has to be larger in the region on the right (where it moves slower, so this agrees with the classical argument above)
In general, if you move to an adjacent region where k is smaller,
your amplitude gets bigger. Adjacent turns out to be critical to this
argument, I need to match
and
for this argument to work. (You can come up with some odd examples where the
amplitude is smaller in a region that has small kinetic energy, if that region
is physically well separated)
Since I should be able to produce any
arbitrary potential as a limit of such "stepwise flat" functions, my argument
should hold quite generally. F+T have an example of the fifth excited state of
a ramp potential (how do I know it's the fifth state?):
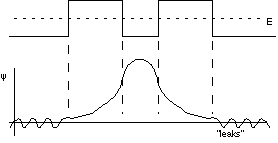
The curve in the middle is no longer a pure sine wave, but is "sine-like". The wavelength is getting continuously longer, and thus broader and taller as it goes to the right. It's a pure exponential decay on the left, and not quite a pure exponential just right of the rightmost classical turning point (do you see why?)
These exponential tails are real consequences of our wave equation, and they turn out to yield most amazing phenomena! It's quite non classical, but it allows trapped particles to leak out of closed containers!
E.g., you could imagine a potential like the following.
(We'll talk about this more later - this is called "tunneling", and all your computer chips and transistors depend on it)
Here is the Next lecture
Back to the list of lectures