Here's how the argument goes:
Inside each step we will have
.
This means that
,
with k2<k1 by inspection. Now, to match the wave functions at the boundary between I and II, and also to match the derivative, we need A2>A1, as claimed above.
Proof:
(F+T have a different, but very similar proof)
In general, if you move to an adjacent region where k is smaller,
your amplitude gets bigger. As I mentioned last time,
adjacent turns out to be critical to this
argument, I need to match
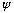and
for this argument to work. (You can come up with some odd examples where the
amplitude is smaller in a region that has small kinetic energy, if that region
is physically well separated) Since I should be able to produce any
arbitrary potential as a limit of such "stepwise flat" functions, this argument
should hold quite generally.
One final issue for this qualitative discussion we're doing: Many potentials, V(x), are symmetric, i.e. V(x) = V(-x).
(There are other, subtler symmetries than this, of course, especially in more
than one dimension) If this is the case, we can argue that particles should be
just as likely to be on one side as the other. But,
Here, I emphasize we're only looking at time independent wave functions. Otherwise, the particle could "slosh" back and forth with time, breaking the symmetry at some particular times.
Anyway, there are two different classes of solutions:
The odd functions always run through the origin. This symmetry property of
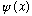is called parity.
If
is even, we say the function has even parity.
If
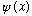is odd, we say it has odd parity.
When doing computer calculations, recognizing symmetry makes life easier! E.g., even wave functions are flat at the origin.
So, you can start at x=0, with some value
,
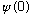and with slope exactly 0, and numerically integrate the Schrodinger equation,
and then if your E gives you
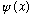going to 0 at infinity, you're happy (and done, except for normalizing).
Alternatively, you can start with
=0,
and pick some value for the slope. But, you needn't ever bother with
different from zero along with slope different from zero. This saves a
lot of unneeded effort! Physicists are always looking for any kind of symmetry
they can, to help ease the work like this! (B.t.w, I study forces (weak forces)
in my research which are not symmetric, so I have to worry about "parity
violating wave functions"!)
Summary of qualitative wave function sketches.
1) Don't worry too much about the norm - we're interested in the basic shape now. (You can always rescale by an overall constant, as we discussed, to properly normalize at the end)
2) If V is symmetric,
better be purely even or odd.
3) The nth level has n-1 nodes, always.
4) As the potential gets higher, (but is still below your energy), your KE drops, so momentum drops, so wavelength gets longer, and amplitude gets bigger. (as long as the potential steps are next to each other)
5) The farther under the potential your energy is outside the well, the faster the wave function must drop towards zero.
(This also affects the behavior of different states of increasing energy)
Here is the Next lecture
Back to the list of lectures