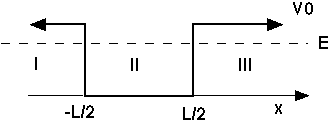
Armed with our ever increasing intuition about what the wave function of bound particles should look like, we can now try to muscle our way through the S.E., and solve (at least one of the simplest cases) analytically! We will begin in the same place our qualitative look did, with the square well.
(Notice the slight change of notation, we don't run from 0 to L, but it's exactly the same potential)
F+T (and these notes, earlier in this section) gave a somewhat artificial example of how to construct such a potential well. But this is pretty much a common potential in many real world situations. A nucleon in the nucleus feels a potential like this. An electron in linear molecules (like H-C---C-H) does too. Or, an electron in a metal foil, as I mentioned before. There are plenty of quantum square wells out there. The first case we're going to solve is when E<V0, so the particle doesn't have enough energy to climb out, so it's trapped in there, or bound.
The S.E. is easy enough to solve in each region independently, we'll just have to see if we can match up the solutions at the boundaries between regions. In regions I and III, we have
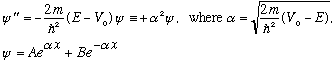
In region I, B=0, or else the wave function would blow up at negative infinity. In region III, A=0, or else it would blow up at plus infinity.
In region II, we have a different equation, because V=0 there:
Let's make our life easier. This potential is clearly symmetric. That is, V(x)=V(-x). So, as we showed earlier, the wave function has to be either even or odd. These are two distinct possibilities, so we'll treat each case separately.
Even parity solutions:
This means we can only have the cos(kx) term, and we have
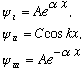
We know the coefficient in region III must also be A, in order for the wave function to be even! We also require that these three different looking functions will have to hook up, so that (as always) the wave function and its first derivative is continuous and finite everywhere.
This means, from continuity of the wave function at -L/2:
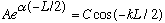
From continuity of the derivative at -L/2:
From continuity of the wave function at the point +L/2:
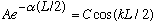
Finally, from continuity of the derivative at +L/2:
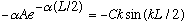
Notice that those last two relations don't provide anything new! The equations are identical to the first two. (That's because we already used symmetry to simplify things. If we hadn't been so clever, we would have needed the additional equations)
Taking the ration of the two equations at -L/2 gives
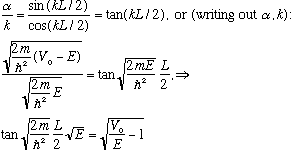
This is an equation in one unknown - E - but I can't solve it! This is called a transcendental equation, I cannot manipulate it in any way to get E=(something algebraically simple). But still, there are solutions!
Recall for a moment the infinite box. There, I had
.
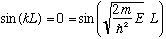This was a fairly similar equation, but it's easier to solve! Indeed, the
solution is
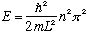
Anyway, how do I find the solutions now? Given m, L, and V0, I could draw a
plot of
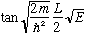vs E, and also
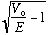vs E, and see at what value(s) of E they cross. This works, but it's a bit
awkward, as I can't get started without knowing all 3 quantities. There's a
better way, it turns out. I can scale my variables, trying to rewrite my
equation in terms of dimensionless unknowns.
So, e.g., let me note that
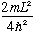has dimensions of (1/Energy),
so
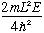(the thing inside a square root inside the tan) is dimensionless,
although it is still proportional to the energy. (It is a sort of dimensionless
energy, if you like!) Let's define a new variable,
.
(This way, I have simply tan(x) on the left hand side)
The right side involves
.
"a" is not a new variable, it is just the combination of fixed, given quantities,
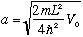
So it turns out that I really don't care what m, L, and V0 are. I only care about the particular combination m L^2 V0 which appears in "a".
We now want to solve
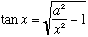for x. If we do that, then we know E.
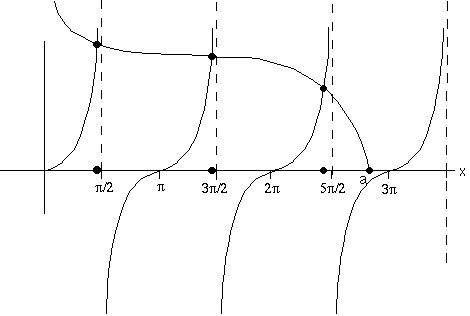
I have plotted tan(x), and
,
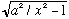where I have picked a particular value for a (slightly less than 3 pi) The tan
x part of the graph is always the same, but the
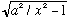curve depends on a, of course. So I'm still sort of stuck (I can't solve the
problem in its most general form like this), but if you give me a value
for a, i.e. for
m L^2 V0, then I can easily draw the plot, find the zero's, and I'm done! In the case shown, there are apparently 3 different solutions for x (the black dots), which means there are 3 and only 3 values of energy that will yield an (even) solution.
Here is the Next lecture
Back to the list of lectures