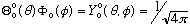
l=0 => m=0 only (since m<=l),
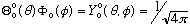
If l=1 => m=-1, 0, or +1. The corresponding solutions are
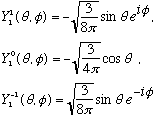
l=2 => m=-2,-1,0,+1, or +2:
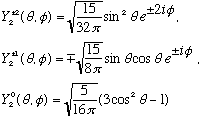
etc...
We won't get into this much more here, but the quantum numbers m and l have
nice simple physical interpretation. Namely, given this wave function,
we could compute the angular momentum of the particle. And we would discover
that the magnitude of the angular momentum vector is roughly
,
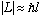while the component of L along the z axis is given by
.
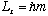These are consistent with the fact that |m|<l, because
(One really finds that if you do it carefully,
)
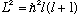You can see Beiser 6.5 for an informal solution, or F+T 11-2 for the formal
proof.
Since V(r) has no dependence on theta or phi, one would expect that all forces lie along the r vector, which means no torques. So angular momentum is conserved, and you should be able to characterize a state by the value of the angular momentum vector, and its component in the z direction (i.e. its orientation). And indeed, we just saw above that is precisely what l and m respectively do for us.
m is often called the magnetic quantum number
l is often called the orbital quantum number.
(orbital for orbital angular momentum, magnetic because magnetic fields turn out to care about what the orientation of your angular momentum is if you're a charged particle)
We're not quite done - we still have to deal with the radial equation! This one explicitly depends on the potential (so it's different for different problems), and it is also the only one which contains the total energy E. It also contains l, but notice that it is independent of m. This means that the total energy won't care about what "m" is; the orientation of angular momentum doesn't affect the energy, as long as the potential is spherically symmetric. (If you add in a magnetic field, it is not spherically symmetric anymore, and the energy does depend on m....)
I remind you of the equation we had, rewritten only slightly:
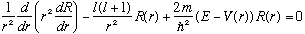
(Again, m in the last term is mass, not the magnetic quantum #)
There's a trick that simplifies this. First, we define a new function
U(r) == r R(r), or equivalently R(r) = U(r)/r.
This means
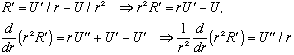
Plugging into the equation above, we get
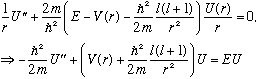
That last equation looks just like a 1-D Schrodinger equation!!
The "effective potential" is weird, it's not V(r), but rather
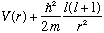
R(r) is what we really need, at the end of the day. It had better not blow up! So, U(0)=0*R(0) = 0. Which means we have a boundary condition on U(r), namely U(0)=0. No matter what!
0<r<infinity, so we can't take advantage of symmetry now. Our U(r) will not be even or odd - it will only be defined for positive r anyway.
Note: Classically, if you move in a circle with angular momentum L, you need an inward force to keep you moving along this path, namely
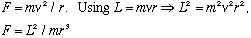
This means you need an extra potential given by
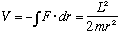
This is a "centripetal potential". That exactly what our extra term looks like,
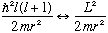
Example: Let l=0, i.e. consider particles with no angular momentum at all. Then, the "effective S.E." we need to solve becomes
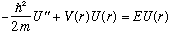
which really looks like an ordinary 1-D S.E.
Sub example: Suppose V(r)=0 up to r=A, and is then infinite. This is an "infinite well", shaped like a sphere instead of like a box. This is not such a bad model for nucleons in a nucleus... So our equation, above, is just identical to a 1-D infinite square well, with the boundary condition that U(0)=0. We have done this as a homework problem - the solution is
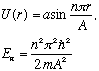
This U clearly satisfies U(0)=0, and also U(A)=0 as required by the fact that the potential goes to infinity there. We can also write down the complete, true wave function in this case:
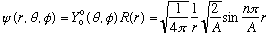
(Note: as r->0, sin(nPi r/A) -> nPi r/A, the r's cancel, and nothing blows up. So, not to worry about that 1/r out front!)
Here is the Next lecture
Back to the list of lectures