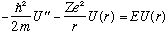
V(r)=-Ze^2/r
Let's begin with the simple case l=0, so we only have to solve the equation
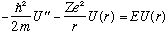
with boundary condition U(0)=0. I can at least sketch the solutions:
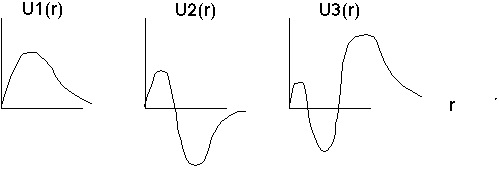
F+T do the quantitative solutions. We won't bother with the derivation, but the approach and solns look quite a bit like harmonic oscillator type solutions (although all the fine details are different):

and the energies are given by
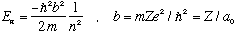
These are precisely the Bohr energies! and the "b", which is some natural (inverse) distance scale in the problem, is just 1/(Bohr radius).
If we stop restricting ourselves to l=0, our radial equation for the hydrogenic potential is
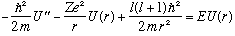
(The first potential term, -Ze^2/r, is as usual a "well". But the second potential term is repulsive, it's positive, so it doesn't help bind particles.) This equation is a bit more painful than the one we had for l=0, and we won't bother solving it here. We certainly could if we wanted to, with much the same approach and techniques as we used for the harmonic oscillator. Some things to note:
If l>0, the potential (including the "centrifugal" term) blows up at the origin. This will force U(r) to go to zero even more strongly than it already did before. So strongly, in fact, that R(r)=U(r)/r itself will even vanish at r=0. (This is not the case for l=0, as we saw explicitly, where R was finite at the origin)
There is a remarkable degeneracy that is occurring. If you look at the solutions we had written down for l=0, which I labeled by n=1,2,3,...
(with corresponding wave function, and also energy En), you discover that for higher l, you get the same allowed energies, exactly! However, for l=1, the n=1 energy is too low - the "centrifugal energy" term requires that you have more energy than that. So, for l=1, you miss out on the n=1 energy level, but match exactly with n=2, 3, ...
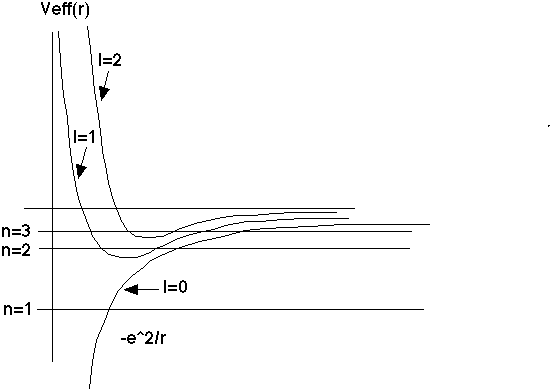
In general, this continues. For l=2, you get exactly the same energies as the old l=0 E_n's, except you skip n=1 and n=2, and start matching starting at n=3,4,... The general rule is, if I give you n (and hence E_n), you can only have solutions if 0 <= l < n
This is a very remarkable feature of the Coulomb potential. In general, you would think that every l could have its own entirely unique spectrum.
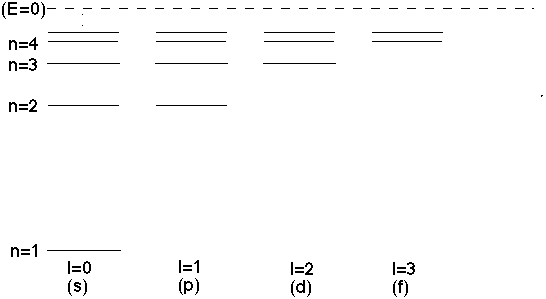
For the l=1 (d) states, each one of the levels I've drawn can have
m=-1,0,+1,
(remember, energy is independent of m), so each of those lines is really 3 fold degenerate.
Similarly, the l=2 (d states) are each 5 fold degenerate. (If you put e.g. a small external magnetic field on the hydrogen atom, you can split those levels, they each get a slightly different energy, and suddenly you see 5 nearby levels instead of 1. This is called "Zeeman splitting".)
Here is the Next lecture
Back to the list of lectures