Issued Wed, Sept 3 Due Wed, Sept 10

Required reading for this week: Gas. Ch. 2, start Ch. 3.

There are HINTS for this homework.
1)

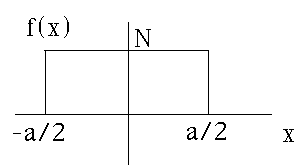
a) A particle is localized in a box of size a, as shown in this figure, i.e. f(x) is uniform (f(x)=N) throughout the box, and zero outside. Use Gas. Eq A-12 (appendix A) to find the Fourier transform of f(x), called A(k)

b) The magnitude of f(x), "N", was not given in part a. Find it, so that your f(x) is properly normalized, i.e. .

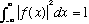c) Given this "N", find the norm of A(k), i.e. .

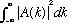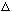d) Sketch A(k). Estimate the "width" of your functions, k and x.

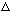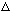Show that kx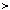1, and this product is independent of "a".

2a) If 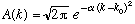, Gas. A-11 (combined with Eq. 2-1 through 2-4) tell us that 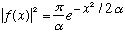, i.e. a particle "located" at x=0. Using all this:

a) what A'(k) would you need to get ,

i.e. a particle "located" at x=x0? (Throughout this problem, you may freely use any results which Gas. has derived, e.g. Eqs 2.1 - 2.17)

b) Is your answer unique? Explain. Is your answer real? Is there anything you could do to make it be real?)

c) Using the A'(k) you got in part a, find |f'(x,t)|^2.

3) Consider the example worked out in Gas. Eq's 2.15 - 2.17, for the "spreading" of a free particle, for which .

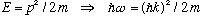Use Gas. Eq. 2-17 (fix his factor 2 errors first!) to find the relative change in the size of a wave packet after one second, if

a) the packet represents an electron, with initial wavepacket size 1 .

b) same, but initial packet size is 10 .

c) the packet represents a Rb atom (atomic #85), initial packet size 1 mm.

d) Describe briefly but as clearly as you can, in words, what the change in the size of the wave packet means, physically.

4) Gas. 2-7

5) Gas. 2-9