1) Look at Gas Fig 1-a. It's sort of the "reverse" of this problem, but because of the symmetry between Fourier transforms and inverse Fourier transforms, the figures you get should like basically the same.

c) You will get a definite integral which is tricky. (If you know about contour integrals, you can solve it) I used Mma (the symbol "Infinity" can be used as a limit of integration in Mma) You can use any reference you like, but tell me what you used.

2) Although you might find it instructive to try, you really do not have to REDO any of the hairy integrals Gas has done for you already! Just think about how you invert Fourier Transforms (be sure to get the factors of 2 Pi right) and think about simple variable changes, and you should be able to find the answer without doing any new integrals. (In fact, with a little thought you might even be able to just guess the answers)

3) Gas. has a bad typo in his constants, the electron mass is 9.1*10^-28 g.

(Though as discussed in class, I never use that number, but instead use

m_e c^2 = 511 keV)

Also, Gas' formula for the width has a mistake in it, I claim:

(we disagree about that factor of 4 in the denominator in the 1st line)

I get very large numbers for parts a and b, and a tiny number for part c.

4) For the ground state, convince yourself that the uncertainty in x ( or p) is roughly equal in magnitude to a typical value of x ( or p) (Can you explain briefly why this is?) The uncertainty principle then relates x and p, so you can eliminate either from the energy equation. (To find the lowest energy, you can differentiate w.r.t. the remaining variable and set to 0... )

5 First, you need to decide if you must use relativity for kinematics here. ( )

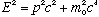As in the previous problem, can you argue that Delta p is roughly p? Why?