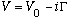Issued Wed, Sept 10 Due Wed, Sept 17

Required reading for this week: Gas. Ch. 3, start Ch. 4.

There are HINTS for this homework.
1) A crude way to model radioactive particles in Q.M. is to assign to the potential, V(x), an imaginary part, .

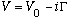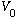( is real, it's the true potential energy. 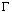is some real, positive, constant)

a) Define the total prob. to find a particle somewhere = 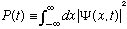Show that (in place of Gas. Eq. 3.13, which assumed V was real) you get

.

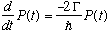b) Solve this equation for P(t), assuming P(0)=1. (Do you see that it looks like radioactive decay?) Find the lifetime of this particle in terms of .

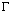2) A particle, mass m, is in the state .

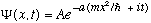"A" and "a" are real, positive, constants.

a) Find A.

b) What must the potential V(x) be, if 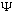is to satisfy the Schrod. Eq'n?

c) Calculate

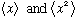
d) Find the momentum space wave fn, 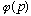. (let t=0, and use Gas 3-26.)

e) Find 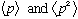in two different ways:

(Method 1) Use , and .

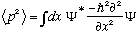(Method 2) Use 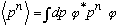. (Methods (1) and (2) should agree!)

f) The uncertainty in any operator O is given by .

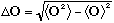Find . Is their product consistent with the uncertainty principle?

3) Gas 3-6.

Does your answer satisfy the uncertainty principle? (Discuss briefly.)

4) Gas 3-8

EXTRA CREDIT PROBLEM:

Prove Ehrenfest's theorem, which states that for any quantum mechanical particle in any real potential V,

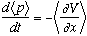
(Note: This makes a nifty connection to classical physics, because classically

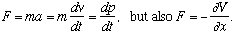
Ehrenfest's theorem says expectation values are obeying Newton's laws!)