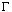1) Gas. has done most of the work for you, pp. 43-44, but he left the potential out of Schrod's Eq! (Don't forget, 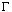is a real, positive, constant.)

b) Technically, 'lifetime" is .

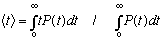("Half life" is simpler to find, but it is not exactly the same as lifetime.)

2a) Is this wave function normalized? It may help you to remember the "Gaussian integral": .

2b) Your answer for V(x) should be a simple, familiar, single term function of x. If you don't get this, you've already made an algebra mistake. (Careful taking derivatives of that exponential - write it out neatly, don't rush through the algebra in this problem or it will kill you in the end!)

2c) Taking derivatives of the "Gaussian integral" above, with respect to "a", is a trick to give you other useful integrals for this problem!

Also, think about symmetry arguments. Never do hard integrals if you can possibly show ahead of time they're going to be zero! There are several places in this problem where symmetry says an integral vanishes!

d) To get 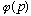, remember how we did the Gaussian Fourier transform in Ch. 2 (Eqs. 2.2 through 2.5) Just be careful about factors of 2 and pi and hbar now, and think carefully about "dummy variables". (You really needn't redo any Gaussian integrals if you don't want to!) If your answers with methods 1 and 2 disagree, you made a mistake. Try to find it!

e) This problem involves Gaussians, and should give the minimum possible uncertainty. (If it doesn't work, you made a mistake. Try to find it!)

3) The main trick here is to figure out 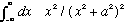. But you know 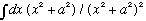(which Gas gives you), and 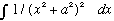(using Gas' suggested trick of taking derivatives), can't you combine these?

4) Gas' statement that 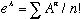is true, but not needed for this exercise! Study eqns. 3.37-38 (but work in p space instead of x space...)

EXTRA CREDIT - This is a somewhat challenging problem, but it's a nice exercise with some useful math, so try it!

You will have to use partial integrations several times in this problem, 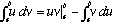. In this equation, the "uv" term is sometimes called a "surface term", because it's evaluated only at the limits of integration, and in this problem you should be able to argue that these surface terms vanish. (Why?!)